题目内容
已知圆锥曲线的一个焦点为
F(1，0)，对应这个焦点的准线方程为x＝－1，且这条曲线经过点M(3，
)．
(Ⅰ)求此圆锥曲线的方程；
(Ⅱ)设直线y＝k(x－4)与圆锥曲线相交于A、B两点，与x轴交于点P，O为坐标原点，若∠AOP＝α，∠BOP＝β，求tanα·tanβ的值．
答案：
解析：
解析：
|
解：（Ⅰ）∵ e＝ ＝1，∴曲线是抛物线…………2分
又∵ F(1，0)，准线x＝－1，∴抛物线顶点在原点 p＝2∴所求的曲线方程为 y2＝4x…………………………………………6分（Ⅱ）当 k＝0时直线与抛物线仅一个交点，不合题意，∴ ¹
0，…8分
把 y＝ ( －4)代入y2＝4 整理得 …10分
设 A(x1，y1)，B(x2，y2)则 ，
 异号， ，……………12分
 …………………………………………………14分
|
练习册系列答案
相关题目
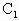的一个焦点为F(1，0)，对应这个焦点的准线方程为x=－1，且曲线
，一条准线的方程为y=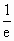
，且中心在原点，求圆锥曲线
的方程．
，0），对应于这个焦点的准线方程为x=-
，0），对应于这个焦点的准线方程为x=-