题目内容
以下命题中:①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②函数f(x)=x
-(
)x在区间(
,
)上存在零点;③设0<x<
,则“sin2x<1”是“xsinx<1”的充分而不必要条件;④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大;其中真命题的个数有( )
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| π |
| 2 |
分析:第一个命题是一个等距抽样,也叫系统抽样;根据题意分别计算出f(
)、f(
),判断它们的符号再结合根的存在性定理可得答案;通过举反例,说明前者成立推不出后者成立;对分类变量X与Y,它们的随机变量K2的观测值k来说,k越大,“X与Y有关系”的把握程度越大.
| 1 |
| 4 |
| 1 |
| 3 |
解答:解:①从匀速传递的产品生产流水线上,
质检员每20分钟从中抽取一件产品进行某项指标检测,是等距抽样,也叫系统抽样,不是分层抽样;故错.
②因为f(
)=(
)
-(
)
<0,f(
)=(
)
-(
)
>0,
所以根据根的存在性定理可得:函数f(x)=x
-(
)x在区间(
,
)上存在零点;故正确;
③设0<x<
,则“sin2x<1”等价于0<sinx<1,若x=2π+
,则“xsinx<1”不成立,故③错;
④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越大,
“X与Y有关系”的把握程度越大,④不正确.
综上可知②正确,
故选C.
质检员每20分钟从中抽取一件产品进行某项指标检测,是等距抽样,也叫系统抽样,不是分层抽样;故错.
②因为f(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
所以根据根的存在性定理可得:函数f(x)=x
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
③设0<x<
| π |
| 2 |
| π |
| 6 |
④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越大,
“X与Y有关系”的把握程度越大,④不正确.
综上可知②正确,
故选C.
点评:本题考查系统抽样,考查独立性检验,考查根的存在性定理,是一个综合题目,这种问题一定要确定每一个命题是否正确.

练习册系列答案
相关题目
 =0.2x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.2个单位;
=0.2x+12中,当解释变量x每增加一个单位时,预报变量平均增加0.2个单位; 的图像向右平移
的图像向右平移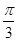 个单位长度可以得到函数
个单位长度可以得到函数 的图像。③在回归直线方程
的图像。③在回归直线方程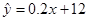 中,当变量x每增加一个单位时,变量
中,当变量x每增加一个单位时,变量 增加0.2单位。④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大。⑤设
增加0.2单位。④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大。⑤设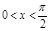 ,则“
,则“ ”是“
”是“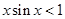 ”的充分而不必要条件。其中为真命题的个数有:
”的充分而不必要条件。其中为真命题的个数有: 在区间
在区间 上存在零点;③设
上存在零点;③设 ,则“sin2x<1”是“xsinx<1”的充分而不必要条件;④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大;其中真命题的个数有
,则“sin2x<1”是“xsinx<1”的充分而不必要条件;④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大;其中真命题的个数有