题目内容
已知sin
+cos
=
,那么cos2θ的值为
.
| θ |
| 2 |
| θ |
| 2 |
2
| ||
| 3 |
| 7 |
| 9 |
| 7 |
| 9 |
分析:通过已知表达式的平方,求出sinθ,利用二倍角的余弦函数,求出结果即可.
解答:解:∵sin
+cos
=
,
∴(sin
+cos
)2=(
)2,
∴sinθ=
,
cos2θ=1-2sin2θ=1-2×(
)2=
.
故答案为:
.
| θ |
| 2 |
| θ |
| 2 |
2
| ||
| 3 |
∴(sin
| θ |
| 2 |
| θ |
| 2 |
2
| ||
| 3 |
∴sinθ=
| 1 |
| 3 |
cos2θ=1-2sin2θ=1-2×(
| 1 |
| 3 |
| 7 |
| 9 |
故答案为:
| 7 |
| 9 |
点评:本题考查同角三角函数的基本关系式,二倍角公式的应用,考查计算能力.

练习册系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E: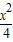
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.