题目内容
14.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,过点F1且垂直于x轴的直线交椭圆C于A、B两点,|AB|=$\frac{4\sqrt{3}}{3}$,△ABF2为正三角形.(1)求椭圆C的标准方程;
(2)记椭圆C的左、右顶点分别为D、E,过点D作直线l依次交椭圆C、直线x=$\sqrt{3}$于M、N两点,若点M位于第一象限,求$\frac{|ME|}{|NE|}$的取值范围.
分析 (1)把x=-c代入椭圆C的方程可得:$y=±\frac{{b}^{2}}{a}$,可得|AB|=$\frac{2{b}^{2}}{a}$=$\frac{4\sqrt{3}}{3}$,于是|AF1|=$\frac{2\sqrt{3}}{3}$,由△ABF2为正三角形,可得|AF2|=2|AF1|.利用2a=|AF2|+|AF1|,解得a.即可得出b2.
(2)设直线l的方程为y=k(x+$\sqrt{3}$),$0<k<\frac{\sqrt{2}}{\sqrt{3}}$.与椭圆方程联立解得M,E( $\sqrt{3}$,0),利用两点之间的距离公式可得|ME|,|NE|.进而得到可得$\frac{|ME|}{|NE|}$,通过换元利用二次函数的单调性即可得出.
解答 解:(1)把x=-c代入椭圆C的方程可得:$y=±\frac{{b}^{2}}{a}$,∴|AB|=$\frac{2{b}^{2}}{a}$=$\frac{4\sqrt{3}}{3}$,∴|AF1|=$\frac{2\sqrt{3}}{3}$,∵△ABF2为正三角形,∴|AF2|=2|AF1|=$\frac{4\sqrt{3}}{3}$.
∴2a=|AF2|+|AF1|=2$\sqrt{3}$,解得a=$\sqrt{3}$.∴b2=2,∴椭圆C的标准方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
(2)解:设直线l的方程为y=k(x+$\sqrt{3}$),$0<k<\frac{\sqrt{2}}{\sqrt{3}}$.
联立$\left\{\begin{array}{l}{y=k(x+\sqrt{3})}\\{2{x}^{2}+3{y}^{2}=6}\end{array}\right.$,化为(2+3k2)x2+6$\sqrt{3}$k2x+9k2-6=0.
解得xM=$\frac{2\sqrt{3}-3\sqrt{3}{k}^{2}}{2+3{k}^{2}}$,
∴yM=$\frac{4\sqrt{3}k}{2+3{k}^{2}}$.
∴M$(\frac{2\sqrt{3}-3\sqrt{3}{k}^{2}}{2+3{k}^{2}},\frac{4\sqrt{3}k}{2+3{k}^{2}})$,
E( $\sqrt{3}$,0),
∴|ME|=$\sqrt{(\frac{2\sqrt{3}-3\sqrt{3}{k}^{2}}{2+3{k}^{2}}-\sqrt{3})^{2}+(\frac{4\sqrt{3}k}{2+3{k}^{2}})^{2}}$=$\frac{2k\sqrt{27{k}^{2}+12}}{2+3{k}^{2}}$.
又N( $\sqrt{3}$,2$\sqrt{3}$k),∴|NE|=2 $\sqrt{3}$k.
∴$\frac{|ME|}{|NE|}$=$\frac{\sqrt{9{k}^{2}+4}}{2+3{k}^{2}}$=f(k),
令2+3k2=t∈(2,4),$\frac{1}{t}$∈$(\frac{1}{4},\frac{1}{2})$.
f(k)=g(t)=$\frac{\sqrt{3t-2}}{t}$=$\sqrt{-2(\frac{1}{t}-\frac{3}{4})^{2}+\frac{9}{8}}$∈$[\frac{\sqrt{10}}{4},1)$.
∴$\frac{|ME|}{|NE|}$的取值范围是$[\frac{\sqrt{10}}{4},1)$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交转化为方程联立可得根与系数的关系、弦长公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.

| A. | {0,1,2} | B. | {0,1} | C. | {x|0<x<2} | D. | {x|-3<x<2} |
| 乘坐里程x(单位:km) | 0<x≤6 | 6<x≤12 | 12<x≤22 |
| 票价(单位:元) | 3 | 4 | 5 |
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量ξ,求ξ的分布列与数学期望.
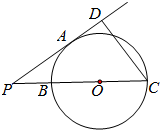 如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.
如图,已知PA是圆O的切线,切点为A,PC过圆心O,且与圆O交于B,C两点,过C点作CD⊥PA,垂足为D,PA=4,BC=6,那么CD=$\frac{24}{5}$.