题目内容
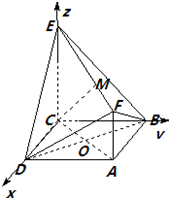
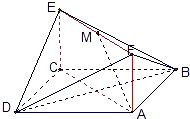
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=2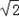 ,CE∥AF,AC⊥CE,
,CE∥AF,AC⊥CE,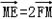
(I)求证:CM∥平面BDF;
(II)求异面直线CM与FD所成角的余弦值的大小;
(III)求二面角A﹣DF﹣B的大小.
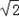 ,CE∥AF,AC⊥CE,
,CE∥AF,AC⊥CE,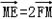
(I)求证:CM∥平面BDF;
(II)求异面直线CM与FD所成角的余弦值的大小;
(III)求二面角A﹣DF﹣B的大小.
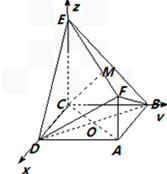
解:(I)证明:因为面ABCD⊥面ACEF,面ABCD∩面ACEF=AC,且AC⊥CE,
∴CE⊥面ABCD.
所以CD、CB、CE两两垂直.可建立如图空间直角坐标系C﹣xyz.
则(2,0,0),A(2,2,0),B(0,2,0),F(2,2,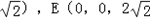 ),O(1,1,0)
),O(1,1,0)
由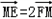 ,可求得M(
,可求得M(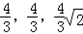 )
)
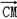 =(
=(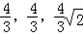 ),
),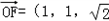 ).
).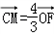
所以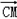 ∥
∥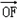 ,
,
∴CM∥OF
∵OF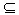 平面BDF
平面BDF
∴CM∥平面BDF 。
(II)因为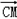 =(
=(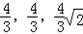 ),
), ),
),
所以cos<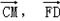 >=
>=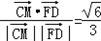
异面直线CM与FD所成角的余弦值的大小为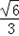
(III)因为CD⊥平面ADF,所以平面ADF的法向量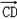 =(2,0,0).
=(2,0,0).
设平面BDF的法向量为 =(x,y,1)
=(x,y,1)
由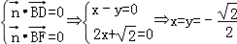 .
.
所以法向量 =(﹣
=(﹣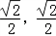 ,1)
,1)
所以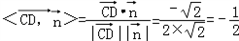 所以<
所以<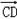
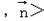 =
=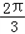 ,
,
由图可知二面角A﹣DF﹣B为锐角,所以二面角A﹣DF﹣B大小为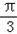 .
.
∴CE⊥面ABCD.
所以CD、CB、CE两两垂直.可建立如图空间直角坐标系C﹣xyz.
则(2,0,0),A(2,2,0),B(0,2,0),F(2,2,
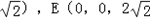 ),O(1,1,0)
),O(1,1,0)由
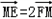 ,可求得M(
,可求得M(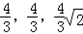 )
)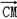 =(
=(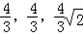 ),
),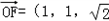 ).
).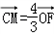
所以
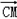 ∥
∥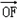 ,
,∴CM∥OF
∵OF
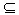 平面BDF
平面BDF∴CM∥平面BDF 。
(II)因为
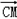 =(
=(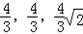 ),
), ),
),所以cos<
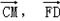 >=
>=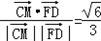
异面直线CM与FD所成角的余弦值的大小为
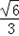
(III)因为CD⊥平面ADF,所以平面ADF的法向量
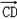 =(2,0,0).
=(2,0,0).设平面BDF的法向量为
 =(x,y,1)
=(x,y,1)由
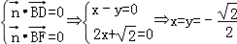 .
.所以法向量
 =(﹣
=(﹣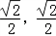 ,1)
,1)所以
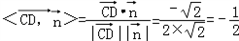 所以<
所以<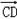
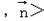 =
=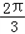 ,
,由图可知二面角A﹣DF﹣B为锐角,所以二面角A﹣DF﹣B大小为
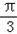 .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.