题目内容
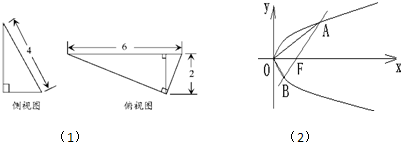
直线 与抛物线
与抛物线 相交于A、B两点,O是抛物线的顶点,若
相交于A、B两点,O是抛物线的顶点,若 ,则
,则 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.
【答案】
A
【解析】
试题分析:顶点是原点
设A( ),B(
),B( )
)
则由OA⊥OB知 =-1
=-1
直线和抛物线相交将方程 代入
代入
整理得 -2x-2b=0
-2x-2b=0
 =2,
=2,  =-2b
=-2b
A和B都在直线上
 =
= +b,
+b,  =
= +b
+b
代入 =-1
=-1
整理可得 =2b
=2b
b=0或b=2
若b=0
则y=x和抛物线只有一个交点,不合题意
所以b=2,选A。
考点:本题主要考查直线与抛物线的位置关系、标准方程及几何性质。
点评:常见题型,注意将联立方程组整理后,运用韦达定理。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目