题目内容
方程 -k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )
-k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )
 -k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )
-k(x-3)+4=0有两个不同的解时,实数k的取值范围是( )A. | B.( ,+∞) ,+∞) | C.( ) ) | D. |
D
先将方程根的情况转化为一个半圆与一条直线交点的情况,再用数形结合,先求出相切时的斜率,再得到有两个交点的情况.
解:将方程 -k(x-3)-4=0转化为:
-k(x-3)-4=0转化为:
半圆 y= ,与直线y=k(x-3)+4有两个不同交点.
,与直线y=k(x-3)+4有两个不同交点.
当直线与半圆相切时,有 =3,即解得:k=
=3,即解得:k=
当半圆y= 与直线y=k(x-3)+4有两个不同交点时,
与直线y=k(x-3)+4有两个不同交点时,
因为直线y=k(x-3)+4一定过点(3,4),
所以由图象知直线过(-3,0)时直线的斜率k取最大值为 ,
,

所以k∈( ,
, ].
].
故选D.
解:将方程
 -k(x-3)-4=0转化为:
-k(x-3)-4=0转化为:半圆 y=
 ,与直线y=k(x-3)+4有两个不同交点.
,与直线y=k(x-3)+4有两个不同交点.当直线与半圆相切时,有
 =3,即解得:k=
=3,即解得:k=
当半圆y=
 与直线y=k(x-3)+4有两个不同交点时,
与直线y=k(x-3)+4有两个不同交点时,因为直线y=k(x-3)+4一定过点(3,4),
所以由图象知直线过(-3,0)时直线的斜率k取最大值为
 ,
,
所以k∈(
 ,
, ].
].故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
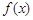 =Atan(
=Atan( x+
x+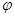 )(
)(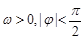 ),y=
),y=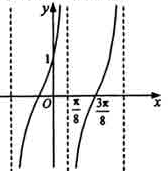
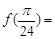


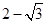
 ,那么( )
,那么( )



 是定义在R上的奇函数,若对于任意给
是定义在R上的奇函数,若对于任意给 、
、 ,不等式
,不等式
 的解集为( ※ )
的解集为( ※ )



 上的函数
上的函数 满足
满足 ,
, ,则不等式
,则不等式 的解集为_____________
的解集为_____________
 ,若
,若 ,则
,则 .
. ( )
( )

 ,且
,且 ,则
,则 的最大值为 .
的最大值为 .  的大致图象,则
的大致图象,则 等于( )
等于( ) B
B  C
C  D
D 
