题目内容
已知a∈R,曲线C1:x2+y2-ax+2ay+a2-a-1=0.
(1)若曲线C1表示圆,求a的取值范围;
(2)当a=2时,求C1所表示曲线关于直线2y+1=0的对称曲线C2的方程;
(3)在第2题条件下,是否存在整数m,使得曲线C1与曲线C2上均恰有两点到直线0≤x≤1时,的距离等于1,若存在,求出m值,若不存在,说明理由.
(1)若曲线C1表示圆,求a的取值范围;
(2)当a=2时,求C1所表示曲线关于直线2y+1=0的对称曲线C2的方程;
(3)在第2题条件下,是否存在整数m,使得曲线C1与曲线C2上均恰有两点到直线0≤x≤1时,的距离等于1,若存在,求出m值,若不存在,说明理由.
分析:(1)化圆的方程为标准方程,利用半径大于0,可求a的取值范围;
(2)确定圆心C1(1,-2)关于直线2y+1=0的对称点为C2(1,1),即可得到C2的方程;
(3)设C1(1,-2)到直线2x+y+m=0的距离为d1,设C2(1,1)到直线2x+y+m=0的距离为d2,则根据d1∈(1,3),d2∈(1,3),结合m为整数,可得结论.
(2)确定圆心C1(1,-2)关于直线2y+1=0的对称点为C2(1,1),即可得到C2的方程;
(3)设C1(1,-2)到直线2x+y+m=0的距离为d1,设C2(1,1)到直线2x+y+m=0的距离为d2,则根据d1∈(1,3),d2∈(1,3),结合m为整数,可得结论.
解答:解:(1)C1:x2+y2-ax+2ay+a2-a-1=0,即(x-
)2+(y+a)2=
+a+1
当
+a+1>0时C1表示圆,此时a2+4a+4>0,∴a≠-2…(3分)
(2)a=2时,C1:(x-1)2+(y+2)2=4,圆心(1,-2)
圆心C1(1,-2)关于直线2y+1=0的对称点为C2(1,1)
圆C2:(x-1)2+(y-1)2=4…(6分)
(3)设C1(1,-2)到直线2x+y+m=0的距离为d1,设C2(1,1)到直线2x+y+m=0的距离为d2,则
∵d1∈(1,3),∴
∈(1,3),∴|m|∈(
,3
),∴m∈(
,3
)∪(-3
,-
)…(9分),
∵d2∈(1,3),∴
∈(1,3),
∴|m+3|∈(
,3
),∴m∈(
-3,3
-3)∪(-3
-3,-
-3)…(12分)
∴m∈(-3
,-
-3)∪(
,3
-3),
又m为整数,∴m=-6或3.…(14分)
所以,存在整数m=-6或3,使得曲线C1与曲线C2上均恰有两点到直线2x+y+m=0的距离等于1 …(15分)
| a |
| 2 |
| a2 |
| 4 |
当
| a2 |
| 4 |
(2)a=2时,C1:(x-1)2+(y+2)2=4,圆心(1,-2)
圆心C1(1,-2)关于直线2y+1=0的对称点为C2(1,1)
圆C2:(x-1)2+(y-1)2=4…(6分)
(3)设C1(1,-2)到直线2x+y+m=0的距离为d1,设C2(1,1)到直线2x+y+m=0的距离为d2,则
∵d1∈(1,3),∴
| |m| | ||
|
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
∵d2∈(1,3),∴
| |m+3| | ||
|
∴|m+3|∈(
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
∴m∈(-3
| 5 |
| 5 |
| 5 |
| 5 |
又m为整数,∴m=-6或3.…(14分)
所以,存在整数m=-6或3,使得曲线C1与曲线C2上均恰有两点到直线2x+y+m=0的距离等于1 …(15分)
点评:本题考查圆的标准方程,考查圆的对称性,考查圆心到直线距离公式的运用,属于中档题.

练习册系列答案
相关题目
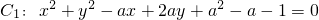 .
.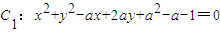 .
.