题目内容
设一元二次不等式ax2+bx+1>0的解集为{x|-1<x<3},则a?b的值为( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
分析:根据一元二次不等式的解集和一元二次方程根之间的关系,即可求出结论.
解答:解:∵一元二次不等式ax2+bx+1>0的解集为{x|-1<x<3},
∴-1,3是对应一元二次方程ax2+bx+1=0的两个根且a<0,
则由根与系数之间的关系可得
,
解得a=-
,b=
,
∴a•b=-
×
=-
,
故选:C.
∴-1,3是对应一元二次方程ax2+bx+1=0的两个根且a<0,
则由根与系数之间的关系可得
|
解得a=-
| 1 |
| 3 |
| 2 |
| 3 |
∴a•b=-
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
故选:C.
点评:本题主要考查一元二次不等式的应用,将一元二次不等式的解集转化为对应一元二次方程根的关系是解决本题的关键,要求熟练掌握三个二次之间的关系.

练习册系列答案
相关题目
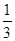 },则ab的值是( )
},则ab的值是( )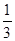 },则ab的值是
_____.
},则ab的值是
_____.