题目内容
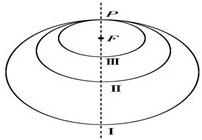
 如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c2;④
| c1 |
| a1 |
| c2 |
| a2 |
其中正确式子的序号是
②③
②③
.分析:根据图象可知a1>a2,c1>c2,进而根据基本不等式的性质分别进行判断即可.可知a1+c1>a2+c2;
>
,进而判断①④不正确.③正确;根据a1-c1=|PF|,a2-c2=|PF|可知a1-c1=a2-c2;
| c1 |
| a1 |
| c2 |
| a2 |
解答:解:由图可知a1>a2,c1>c2,∴a1+c1>a2+c2,∴①不正确,
∵a1-c1=|PF|,a2-c2=|PF|,∴a1-c1=a2-c2,∴②正确.
a1+c2=a2+c1,可得(a1+c2)2=(a2+c1)2,
a12-c12+2a1c2=a22-c22+2a2c1,
即b12+2a1c2=b22+2a2c1,
∵b1>b2,∴c1a2>a1c2,∴③正确;
此时
>
,∴④不正确.
故答案为:②③.
∵a1-c1=|PF|,a2-c2=|PF|,∴a1-c1=a2-c2,∴②正确.
a1+c2=a2+c1,可得(a1+c2)2=(a2+c1)2,
a12-c12+2a1c2=a22-c22+2a2c1,
即b12+2a1c2=b22+2a2c1,
∵b1>b2,∴c1a2>a1c2,∴③正确;
此时
| c1 |
| a1 |
| c2 |
| a2 |
故答案为:②③.
点评:本题主要考查了椭圆的简单性质.以及不等式的性质的应用,考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
相关题目
 如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子: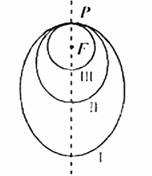
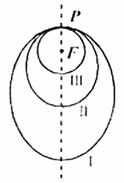 ①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c2;④
①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c2;④