题目内容
(本小题满分15分)已知函数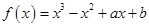 (
(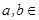 R)的一个极值点为
R)的一个极值点为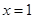 .
.
(1) 求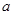 的值和
的值和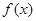 的单调区间;
的单调区间;
(2) 若方程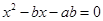 的两个实根为
的两个实根为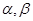
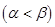 , 函数
, 函数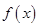 在区间
在区间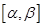 上单调,求
上单调,求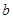 的取值范围。
的取值范围。
【答案】
(1)函数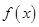 在
在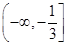 上单调递增, 在
上单调递增, 在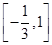 上单调递减,在
上单调递减,在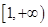 上单调递增. (2)实数
上单调递增. (2)实数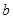 的取值范围为
的取值范围为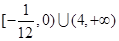 .
.
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)因为函数的一个极值点为x=1.
可以知道该点的导数值为零,得到a的值,并进而求解导数,得到f(x)的单调区间;
(2) 因为方程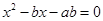 的两个实根为
的两个实根为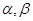 , 函数f(x)在区间
, 函数f(x)在区间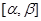 上单调,利用单调性判定区间只能是已知单调区间的子区间而已,进而求解得到范围。
上单调,利用单调性判定区间只能是已知单调区间的子区间而已,进而求解得到范围。
解:(1)∵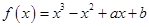 ,
,
∴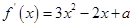 .
.
∵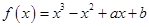 的一个极值点为
的一个极值点为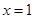 ,
,
∴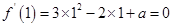 .
.
∴ 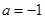 .
————————3分
.
————————3分
∴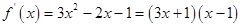 ,
,
当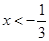 时,
时, 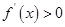 ;当
;当 时,
时, 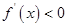 ;当
;当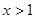 时,
时, 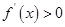 ;
;
∴函数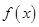 在
在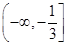 上单调递增, 在
上单调递增, 在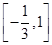 上单调递减,在
上单调递减,在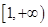 上单调递增. 6分
上单调递增. 6分
(2)∵方程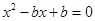 的两个不等实根为
的两个不等实根为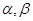 ,
,
∴△=b2-4b>0, b<0或b>4 (*)
∵ 函数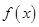 在区间
在区间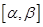 上是单调的,
上是单调的,
∴区间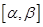 只能是区间
只能是区间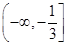 ,
,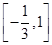 ,
,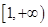 之一的子区间.
之一的子区间.
记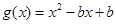 ,
,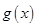 的对称轴为x=
的对称轴为x=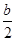 ,
,
①.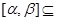
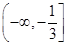 , 则
, 则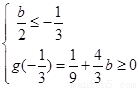 ,解得无解;————————9分
,解得无解;————————9分
②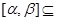
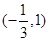 ,则
,则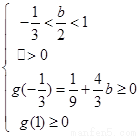 ,解得
,解得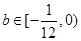 ———————12分
———————12分
③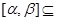
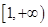 则
则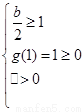 解得b>4
解得b>4
∴实数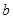 的取值范围为
的取值范围为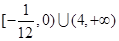 .
------------------------------------------------15分
.
------------------------------------------------15分

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.