题目内容
从10人(含甲、乙)中选出4人参加某项公益活动,要求甲、乙二人中至少有1人参加,则不同选法有
- A.210
- B.168
- C.180
- D.140
D
分析:由题意,事件“甲、乙中至少有1人参加”的对立事件是“两人都不参加”,故本题在求解时可以用排除法,先求出10名同学中挑选4名参加某项公益活动的选法,再计算出甲乙两人都不参数的选法,总数中排除掉甲乙两人都不参数的选法,即可得事件“甲、乙中至少有1人参加”的种数.
解答:10名同学中挑选4名参加某项公益活动,总的选法有C104=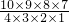 =210种,
=210种,
甲乙两人都不参数的选法有C84=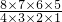 =70种,
=70种,
故事件“甲、乙中至少有1人参加”包含的基本事件数是210-70=140.
故选D.
点评:本题考查排列组合及简单计数问题,解题的关键是理解事件“甲、乙中至少有1人参加”,将问题转化为求其对立事件包含的基本事件数,此技巧在计数问题在经常使用,适合于求所研究的事件分类较多,而其对立事件包含的类较少的情况,方便计数.
分析:由题意,事件“甲、乙中至少有1人参加”的对立事件是“两人都不参加”,故本题在求解时可以用排除法,先求出10名同学中挑选4名参加某项公益活动的选法,再计算出甲乙两人都不参数的选法,总数中排除掉甲乙两人都不参数的选法,即可得事件“甲、乙中至少有1人参加”的种数.
解答:10名同学中挑选4名参加某项公益活动,总的选法有C104=
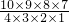 =210种,
=210种,甲乙两人都不参数的选法有C84=
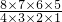 =70种,
=70种,故事件“甲、乙中至少有1人参加”包含的基本事件数是210-70=140.
故选D.
点评:本题考查排列组合及简单计数问题,解题的关键是理解事件“甲、乙中至少有1人参加”,将问题转化为求其对立事件包含的基本事件数,此技巧在计数问题在经常使用,适合于求所研究的事件分类较多,而其对立事件包含的类较少的情况,方便计数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目