题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切. ![]() 、
、![]() 是椭圆
是椭圆![]() 的右顶点与上顶点,直线
的右顶点与上顶点,直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点.
两点.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当四边形![]() 面积取最大值时,求
面积取最大值时,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() =2.
=2.
【解析】试题分析:(1)利用离心率和直线与圆相切以及![]() 的关系进行求解;(2)设
的关系进行求解;(2)设![]() ,联立直线与椭圆方程,得到
,联立直线与椭圆方程,得到![]() 的横坐标,求出点
的横坐标,求出点![]() 到直线
到直线![]() 的距离,得到四边形面积关于
的距离,得到四边形面积关于![]() 的表达式,再利用基本不等式进行求解.
的表达式,再利用基本不等式进行求解.
试题解析:(Ⅰ)由题意知: ![]() =
=![]()
![]()
![]() ,
, ![]() .
.
又圆![]() 与直线
与直线![]() 相切,
相切, ![]() ,
, ![]() ,
,
故所求椭圆![]() 的方程为
的方程为![]() .
.
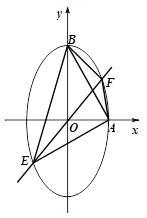
(Ⅱ)设![]() ,其中
,其中![]() ,
,
将![]() 代入椭圆的方程
代入椭圆的方程![]() 整理得:
整理得: ![]() ,
,
故![]() .①
.①
又点![]() 到直线
到直线![]() 的距离分别为
的距离分别为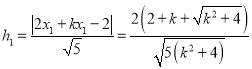 ,
,
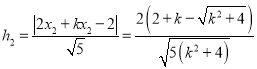 ,
, ![]()
所以四边形![]() 的面积为
的面积为
![]()
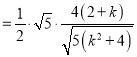
![]()
![]()
![]()
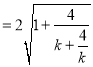
![]() ,
,
当![]() ,即当
,即当![]() 时,上式取等号,所以当四边形
时,上式取等号,所以当四边形![]() 面积的最大值时,
面积的最大值时, ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


