题目内容
如图所示,在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ(1)求△ABC的面积f(θ)与正方形面积g(θ);
(2)当θ变化时,求
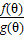 的最小值.
的最小值.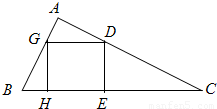
【答案】分析:(1)设正方形边长为x,求出BG= ,AC=atanθ,x,即可求出三角形ABC的面积f(θ)与正方形面积g(θ);
,AC=atanθ,x,即可求出三角形ABC的面积f(θ)与正方形面积g(θ);
(2)利用(1)推出 的表达式,利用基本不等式,求出比值的最小值即可.
的表达式,利用基本不等式,求出比值的最小值即可.
解答:解:(1)由题得:AC=atanθ
∴f(θ)= a2tanθ(0<θ<
a2tanθ(0<θ< )
)
设正方形的边长为x,则BG= ,由几何关系知:∠AGD=θ
,由几何关系知:∠AGD=θ
∴AG=xcosθ 由BG+AG=a⇒ ⇒x=
⇒x=
∴g(θ)= (0<θ<
(0<θ< )
)
(2) =
= =1+
=1+ +
+ 令:t=sin2θ
令:t=sin2θ
∵0<θ<
∴t∈(0,1]∴y=1+ =1+
=1+ (t+
(t+ )∵函数y=1+
)∵函数y=1+ (t+
(t+ )在(0,1]递减
)在(0,1]递减
∴ymin= (当且仅当t=1即θ=
(当且仅当t=1即θ= 时成立)
时成立)
∴当θ= 时,
时, 的最小值为
的最小值为 .
.
点评:本题主要考查三角函数的基本关系式,基本不等式的应用,同时考查了计算能力,属于中档题.
 ,AC=atanθ,x,即可求出三角形ABC的面积f(θ)与正方形面积g(θ);
,AC=atanθ,x,即可求出三角形ABC的面积f(θ)与正方形面积g(θ);(2)利用(1)推出
 的表达式,利用基本不等式,求出比值的最小值即可.
的表达式,利用基本不等式,求出比值的最小值即可.解答:解:(1)由题得:AC=atanθ
∴f(θ)=
 a2tanθ(0<θ<
a2tanθ(0<θ< )
) 设正方形的边长为x,则BG=
 ,由几何关系知:∠AGD=θ
,由几何关系知:∠AGD=θ∴AG=xcosθ 由BG+AG=a⇒
 ⇒x=
⇒x=
∴g(θ)=
 (0<θ<
(0<θ< )
)(2)
 =
= =1+
=1+ +
+ 令:t=sin2θ
令:t=sin2θ∵0<θ<

∴t∈(0,1]∴y=1+
 =1+
=1+ (t+
(t+ )∵函数y=1+
)∵函数y=1+ (t+
(t+ )在(0,1]递减
)在(0,1]递减∴ymin=
 (当且仅当t=1即θ=
(当且仅当t=1即θ= 时成立)
时成立)∴当θ=
 时,
时, 的最小值为
的最小值为 .
.点评:本题主要考查三角函数的基本关系式,基本不等式的应用,同时考查了计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 22、如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC.
22、如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC. 如图所示,在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ
如图所示,在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ 如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
 如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC.
如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC.