题目内容
19.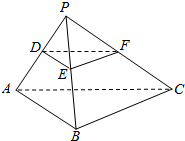 已知D,E,F分别是三棱锥P-ABC的棱PA,PB,PC的中点,求证:平面DEF∥平面ABC.
已知D,E,F分别是三棱锥P-ABC的棱PA,PB,PC的中点,求证:平面DEF∥平面ABC.
分析 由三角形中位线定理得DE∥AB,EF∥BC,由此能证明平面DEF∥平面ABC.
解答 解:∵D,E,F分别是三棱锥P-ABC的棱PA,PB,PC的中点,
∴DE∥AB,EF∥BC,
∵DE∩EF=E,AB∩BC=B,
DE?平面DEF,EF?平面DEF,AB?平面ABC,BC?平面ABC,
∴平面DEF∥平面ABC.
点评 本题考查面面平行的证明,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
9.一个几何体的三视图如图所示,其中俯视图与侧视图都是半径为2的圆,则这个几何体的体积是( )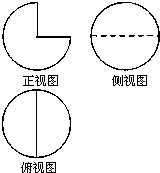

| A. | 8π | B. | 16π | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
11.已知该球的直径SC=8,A,B是该球球面上的两点,AB=2$\sqrt{3}$,∠SCA=∠SCB=60°,则球心O到平面ABC的距离为( )
| A. | 4$\sqrt{3}$ | B. | $\frac{24\sqrt{13}}{13}$ | C. | $\frac{12\sqrt{13}}{13}$ | D. | 8$\sqrt{3}$ |
8.已知函数f(x)=x-[x],其中[x]表示不超过实数x的最大整数,若函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是( )
| A. | (-1,-$\frac{1}{3}$] | B. | [$\frac{1}{5}$,$\frac{1}{3}$) | C. | (-$\frac{1}{3}$,-$\frac{1}{2}$]∪[$\frac{1}{5}$,$\frac{1}{4}$) | D. | [$\frac{1}{4}$,$\frac{1}{3}$] |
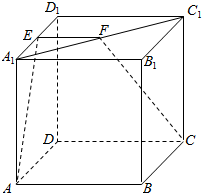 如图,正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,求:
如图,正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,求: 如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.
如图,矩形ABDE所在平面与正三角形ABC所在平面互相垂直,AE=3,AB=2$\sqrt{3}$,点O是边AB的中点.