题目内容
5.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
分析 连接DE,连接并延长EP交BC于点F,利用DE是△ABC中位线,求出FC=$\frac{1}{2}$BC,再用PQ是△EFC中位线,PQ=$\frac{1}{2}$CF,即可求得答案.
解答 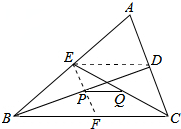 解:连接DE,连接并延长EP交BC于点F,
解:连接DE,连接并延长EP交BC于点F,
∵DE是△ABC中位线,
∴DE=$\frac{1}{2}$BC,AE=BE,AD=CD,
∴∠EDB=∠DBF,
∵P、Q是BD、CE的中点,
∴DP=BP,
∵在△DEP与△BFP中,∠EDB=∠DBF,DP=BP,∠EPD=∠BPF,
∴△DEP≌△BFP(ASA),
∴BF=DE=$\frac{1}{2}$BC,P是EF中点,
∴FC=$\frac{1}{2}$BC,
PQ是△EFC中位线,PQ=$\frac{1}{2}$FC,
∴PQ:BC=1:4.
故选:B.
点评 本题考查两线段比值的求法,是中档题,解题时要认真审题,注意三角形中位线定理的合理运用.

练习册系列答案
相关题目
17.在棱长为$\sqrt{6}$的正方体ABCD-A1B1C1D1中,D1到B1C的距离为( )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
14.某中学高二年级举行数学竞赛,共有800名学生参加.为了了解本次竞赛成绩,从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计.请你根据频率分布表,解答下列问题:
(1)填充下列频率分布表中的空格;
(2)估计众数、中位数和平均数;
(3)规定成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名学生获奖?
(1)填充下列频率分布表中的空格;
(2)估计众数、中位数和平均数;
(3)规定成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名学生获奖?
| 分组(分数) | 频数 | 频率 |
| [60,70) | 0.12 | |
| [70,80) | 20 | |
| [80,90) | 0.24 | |
| [90,100] | 12 | |
| 合计 | 50 | 1 |
15.已知球O的表面积为12π,则球O的体积为( )
| A. | 2$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 12$\sqrt{3}$π | D. | 32$\sqrt{3}$π |
 如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB.PA=PB=AB=BC=6,点M,N分别为PB,BC的中点.