题目内容
18.函数f(x)=$\frac{sinx}{|cosx|}$在区间[-π,π]内的大致图象是如图所示的( )| A. |  | B. |  | C. |  | D. |  |
分析 化简f(x)=$\frac{sinx}{|cosx|}$=$\left\{\begin{array}{l}{-tanx,-π≤x<-\frac{π}{2}或\frac{π}{2}<x≤π}\\{tanx,-\frac{π}{2}<x<\frac{π}{2}}\end{array}\right.$,从而作函数的图象即可.
解答 解:f(x)=$\frac{sinx}{|cosx|}$=$\left\{\begin{array}{l}{-tanx,-π≤x<-\frac{π}{2}或\frac{π}{2}<x≤π}\\{tanx,-\frac{π}{2}<x<\frac{π}{2}}\end{array}\right.$;
作函数的图象如下,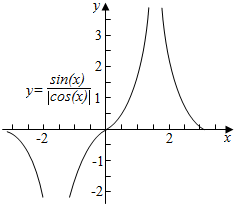
故选:B.
点评 本题考查了函数的化简与函数的图象的作法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.如图,四边形ABCD是边长为1的正方形,延长CD至E,使得DE=2CD,动点P从点A出发,沿正方形的边按逆时针方向运动到C点,$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+μ$\overrightarrow{AE}$,若$\overrightarrow{AE}$•$\overrightarrow{AP}$=-$\frac{5}{3}$,则λ+μ=( )


| A. | $\frac{5}{6}$ | B. | 1或2 | C. | $\frac{5}{6}$或2 | D. | 1或$\frac{5}{6}$ |
6.将y=f(x)图象上的每一点的纵坐标保持不变,横坐标变为原来的$\frac{1}{2}$,再将其图象沿x轴向左平称$\frac{π}{6}$个单位,得到的曲线与y=sin2x的图象相同,则f(x)的解析式为( )
| A. | y=sin(4x-$\frac{π}{3}$) | B. | y=sin(x-$\frac{π}{6}$) | C. | y=sin(4x+$\frac{π}{3}$) | D. | y=sin(x-$\frac{π}{3}$) |
10.函数y=x3-lnx在x=1处的切线方程为( )
| A. | 2x+y-1=0 | B. | 2x+y+1=0 | C. | 2x-y-1=0 | D. | 2x-y+1=0 |