题目内容
在正方体ABCD-A1B1C1D1的面A1B1C1D1内任取一点S，作四棱锥S-ABCD，在正方体内随机取一点M，那么点M落在S-ABCD内部的概率是（ ）A．
B．
C．
D．
【答案】分析：四棱锥S-ABCD与正方体ABCD-A1B1C1D1底面积相等，高也相等，根据锥体的体积公式可得四棱锥S-ABCD的体积等于正方体ABCD-A1B1C1D1体积的
，由此利用几何概型计算公式即可算出所求的概率．
解答：解：∵四棱锥S-ABCD的底面为正方体ABCD，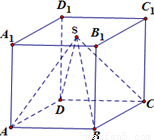
点S到平面ABCD的距离等于正方体的棱长
∴四棱锥S-ABCD与正方体ABCD-A1B1C1D1底面积相等，高也相等
因此VS-ABCD=
VABCD-A1B1C1D1
可得在正方体内随机取一点M，那么点M落在S-ABCD内部的概率为
P=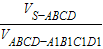
=
故选：D
点评：本题给出正方体内的四棱锥，求正方体内取一点可以落在四棱锥内部的概率．着重考查了正方体的性质、锥体体积公式和几何概型及其应用等知识，属于基础题．
，由此利用几何概型计算公式即可算出所求的概率．解答：解：∵四棱锥S-ABCD的底面为正方体ABCD，
点S到平面ABCD的距离等于正方体的棱长
∴四棱锥S-ABCD与正方体ABCD-A1B1C1D1底面积相等，高也相等
因此VS-ABCD=
VABCD-A1B1C1D1可得在正方体内随机取一点M，那么点M落在S-ABCD内部的概率为
P=
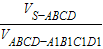=故选：D
点评：本题给出正方体内的四棱锥，求正方体内取一点可以落在四棱锥内部的概率．着重考查了正方体的性质、锥体体积公式和几何概型及其应用等知识，属于基础题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）