题目内容
已知两个点M(-5,0)和N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“B型直线”,给出下列直线:①y=x+1;②y=| 4 | 3 |
分析:根据题设条件可知点P的轨迹方程是
-
=1(x>0),将直线①,②,③,④的方程分别与
-
=1(x>0)联立,若方程组有解,则该直线为“B型直线”.
| x2 |
| 9 |
| y2 |
| 16 |
| x2 |
| 9 |
| y2 |
| 16 |
解答:解:∵|PM|-|PN|=6∴点P在以M、N为焦点的双曲线的右支上,即
-
=1(x>0),
①
,把y=x+1代入双曲线
-
=1(x>0)并整理,得7x2-18x-153=0,∵△=(-18)2-4×7×(-153)>0∴y=x+1是“B型直线”.
②
,把y=
x代入双曲线
-
=1(x>0)并整理,得144=0,不成立.∴y=
x不是“B型直线”.
③
,把y=2代入双曲线
-
=1(x>0)并整理,得x2=
,∴y=2是“B型直线”.
④
,把y=2x+1代入双曲线
-
=1(x>0)并整理,得20x2+36x+153=0,∵△=362-4×20×153<0∴y=2x+1不是“B型直线”.
答案:①③.
| x2 |
| 9 |
| y2 |
| 16 |
①
|
| x2 |
| 9 |
| y2 |
| 16 |
②
|
| 4 |
| 3 |
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
③
|
| x2 |
| 9 |
| y2 |
| 16 |
| 45 |
| 4 |
④
|
| x2 |
| 9 |
| y2 |
| 16 |
答案:①③.
点评:将直线①,②,③,④的方程分别与
-
=1(x>0)联立,若方程组有解,则该直线为“B型直线”.
| x2 |
| 9 |
| y2 |
| 16 |

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知两个点M(-5,0)和N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“B型直线”,给出下列直线是“B型直线”的是( )
| A、y=x+1 | ||
B、y=
| ||
C、y=-
| ||
| D、y=2x+1 |
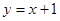 ;②
;②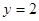 ;③
;③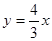 ;④
;④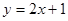 .其中为“B型直线”的是
( )
.其中为“B型直线”的是
( )