题目内容
(本小题满分14分)
设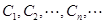 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在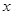 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线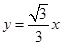 相切,对每一个正整数
相切,对每一个正整数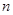 ,圆
,圆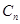 都与圆
都与圆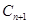 相互外切,以
相互外切,以 表示
表示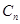 的半径,已知
的半径,已知 为递增数列.
为递增数列.
(1)证明: 为等比数列;
为等比数列;
(2)设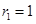 ,求数列
,求数列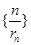 的前
的前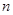 项和.
项和.
【答案】
(1)略
(2)Sn= –
– (n+
(n+ )·
)·
【解析】解:(Ⅰ)将直线y= x的倾斜角记为
x的倾斜角记为 ,
,
则有tan =
=  ,sin
,sin =
= .………….1分
.………….1分
设Cn的圆心为( ,0),则由题意知
,0),则由题意知 = sin
= sin =
= ,
,
得 = 2
= 2 ; ………
………….3分
; ………
………….3分
同理 ,依题意知
,依题意知 ………………5分
………………5分
将 = 2
= 2 代入,
代入,
解得 rn+1=3rn.
故{ rn }为公比q=3的等比数列. ………………7分
(Ⅱ)由于r1=1,q=3,故rn=3n-1,从而 =n·
=n· ,………………9分
,………………9分
记Sn= ,
,
则有
Sn=1+2·3-1+3·3-2+………+n· . ①
. ①
 =1·3-1+2·3-2+………+(n-1) ·
=1·3-1+2·3-2+………+(n-1) · +n·
+n· . ② ………………11分
. ② ………………11分
①-②,得
 =1+3-1
+3-2+………+
=1+3-1
+3-2+………+ -n·
-n· ………………………12分
………………………12分
= - n·
- n·
= –(n+
–(n+ )·
)· ………………………………13分
………………………………13分
Sn= –
– (n+
(n+ )·
)· .
………………………………14分
.
………………………………14分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)