题目内容
已知函数 ,
,
(1)判断函数 的奇偶性;
的奇偶性;
(2)求函数 的单调区间;
的单调区间;
(3)若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围
的取值范围
【答案】
(1)偶函数;(2)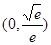 ,
,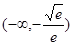 ;(3)
;(3)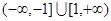
【解析】
试题分析:(1)判断奇偶性,需先分析函数的定义域要关于原点对称,然后分析解析式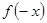 与
与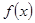 的关系可得;(2)根据偶函数在对称区间上的单调性相反,所以可以考虑先分析
的关系可得;(2)根据偶函数在对称区间上的单调性相反,所以可以考虑先分析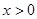 时的单调性,于是在
时的单调性,于是在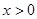 时利用导数分析函数的单调性,然后再分析对称区间上的单调性;(3)把方程的根转化为函数的零点,然后利用导数分析函数的最值,保证函数图形与
时利用导数分析函数的单调性,然后再分析对称区间上的单调性;(3)把方程的根转化为函数的零点,然后利用导数分析函数的最值,保证函数图形与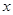 的交点的存在
的交点的存在
试题解析:(1)函数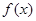 的定义域为
的定义域为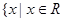 且
且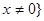 关于坐标原点对称 1分
关于坐标原点对称 1分
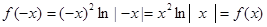
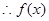 为偶函数
4分
为偶函数
4分
(2)当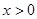 时,
时,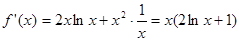 5分
5分
令

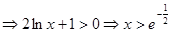
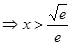
令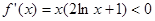
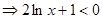
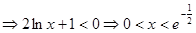
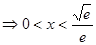 6分
6分
所以可知:当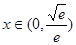 时,
时,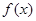 单调递减,
单调递减,
当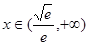 时,
时,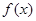 单调递增,
7分
单调递增,
7分
又因为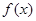 是偶函数,所以在对称区间上单调性相反,所以可得:
是偶函数,所以在对称区间上单调性相反,所以可得:
当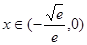 时,
时,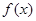 单调递增,
单调递增,
当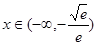 时,
时,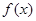 单调递减,
8分
单调递减,
8分
综上可得: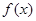 的递增区间是:
的递增区间是: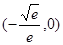 ,
,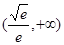 ;
;
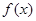 的递减区间是:
的递减区间是: 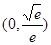 ,
,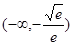 10分
10分
(3)由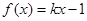 ,即
,即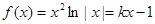 ,显然,
,显然,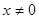
可得: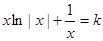 令
令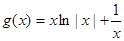 ,当
,当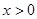 时,
时,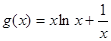
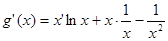
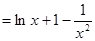
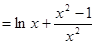 12分
12分
显然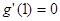 ,当
,当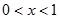 时,
时,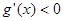 ,
,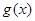 单调递减,
单调递减,
当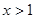 时,
时,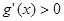 ,
,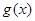 单调递增,
单调递增,
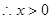 时,
时,  14分
14分
又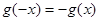 ,所以可得
,所以可得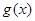 为奇函数,所以
为奇函数,所以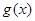 图像关于坐标原点对称
图像关于坐标原点对称
所以可得:当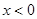 时,
时,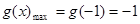 16分
16分
∴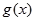 的值域为
的值域为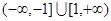 ∴
∴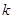 的取值范围是
的取值范围是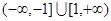 16分
16分
考点:奇偶性,导数,函数的单调性,函数的最值

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

 (理)已知函数
(理)已知函数
 ,有h(h(a))=a;
,有h(h(a))=a;
 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围; 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
 (理)已知函数
(理)已知函数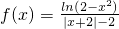 .
.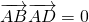 ,求D2+E2-4F的值;
,求D2+E2-4F的值; .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;
