题目内容
动点A（x，y）在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转，12秒旋转一周．已知时间t=0时，点A的坐标是(
，
)，则当0≤t≤12时，动点A的纵坐标y关于t（单位：秒）的函数的单调递增区间是（ ）
| 1 |
| 2 |
| ||
| 2 |
| A、[0，1] |
| B、[1，7] |
| C、[7，12] |
| D、[0，1]和[7，12] |
分析：由动点A（x，y）在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转，可知与三角函数的定义类似，由12秒旋转一周能求每秒钟所转的弧度，画出单位圆，很容易看出，当t在[0，12]变化时，点A的纵坐标y关于t（单位：秒）的函数的单调性的变化，从而得单调递增区间．
解答：解：设动点A与x轴正方向夹角为α，则t=0时α=
，每秒钟旋转
，在t∈[0，1]上α∈[
，
]，在[7，12]上α∈[
，
]，动点A的纵坐标y关于t都是单调递增的．
故选D．
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| 7π |
| 3 |
故选D．
点评：本题主要考查通过观察函数的图象确定函数单调性的问题．
练习册系列答案
阅读快车系列答案
相关题目
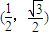，则当0≤t≤12时，动点A的纵坐标y关于t（单位：秒）的函数的单调递增区间是（ ）