题目内容
下列函数在(-1,1)内既是奇函数又是增函数的是( )
分析:由函数的定义域可判断出A、B错误,再由正弦函数的单调性判断出C正确,根据二次函数的对称性和函数奇偶性判断出D不对.
解答:解:A、函数y=-
的定义域是{x|x≠0},则A不对;
B、函数y=log2x的定义域是{x|x>0},则B不对;
C、函数y=sinx是奇函数,在[-
,
]上递增,则在(-1,1)上递增,则c正确;
D、由函数y=(x+2)2的对称轴是x=-2知,此函数不是奇函数,则D不对,
故选C.
| 1 |
| x |
B、函数y=log2x的定义域是{x|x>0},则B不对;
C、函数y=sinx是奇函数,在[-
| π |
| 2 |
| π |
| 2 |
D、由函数y=(x+2)2的对称轴是x=-2知,此函数不是奇函数,则D不对,
故选C.
点评:本题考查了基本初等函数的性质;:定义域、奇偶性和单调性的应用,应熟练掌握这些性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
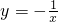

 (1-x2)
(1-x2)