题目内容
某学生对函数f(x)=xsinx进行研究后,得出如下四个结论:①函数f(x)在［-
,
］上单调递增;②存在常数M＞0,使|f(x)|≤M|x|对一切实数x均成立;③函数f(x)在(0,π)上无最小值,但一定有最大值;④点(π,0)是函数y=f(x)图象的一个对称中心.其中正确的是A.①③ B.②③ C.②④ D.①②④
B
解:∵f′(x)=sinx+xcosx,
当x∈［-,0)时f′(x)＜0,∴①错.
由|f(x)|≤M|x|,则|x|·|sinx|≤M|x|,
即M≥|sinx|.
而|sinx|≤1,∴存在常数M＞0使其成立.故②正确.
又∵f(x)=xsinx在(0,π)上先增后减,∴③正确.故选B.
练习册系列答案
金博士一点全通系列答案
相关题目
上单调递增；
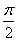，0)是函数y＝f(x)图象的一个对称中心；
，0）是函数y=f(x)图像的一个对称中心；
，0）是函数f（x）图象的一个对称中心；