题目内容
已知不等式(x﹣1)2≤a2,(a>0)的解集为A,函数 的定义域为B.
的定义域为B.
(Ⅰ)若A∩B= ,求a的取值范围;
,求a的取值范围;
(Ⅱ)证明函数 的图象关于原点对称.
的图象关于原点对称.
 的定义域为B.
的定义域为B.(Ⅰ)若A∩B=
 ,求a的取值范围;
,求a的取值范围;(Ⅱ)证明函数
 的图象关于原点对称.
的图象关于原点对称.解:(Ⅰ)由(x﹣1)2≤a2,(a>0),得1﹣a≤x≤1+a,
A={x|1﹣a≤x≤1+a},
由 >0得x<﹣2或x>2,
>0得x<﹣2或x>2,
B={x|x<﹣2或x>2},
∵A∩B= ,
,
∴﹣2≤1﹣a且1+a≤2(a>0),
∴0<a≤1;
(Ⅱ)证明:∵ (x<﹣2或x>2),∴
(x<﹣2或x>2),∴
∴f(﹣x)=﹣f(x),
∴f(x)为奇函数,
∴f(x)的图象关于原点对称.
A={x|1﹣a≤x≤1+a},
由
 >0得x<﹣2或x>2,
>0得x<﹣2或x>2,B={x|x<﹣2或x>2},
∵A∩B=
 ,
,∴﹣2≤1﹣a且1+a≤2(a>0),
∴0<a≤1;
(Ⅱ)证明:∵
 (x<﹣2或x>2),∴
(x<﹣2或x>2),∴
∴f(﹣x)=﹣f(x),
∴f(x)为奇函数,
∴f(x)的图象关于原点对称.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
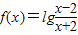 的定义域为B.
的定义域为B.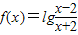 的图象关于原点对称.
的图象关于原点对称.