题目内容

在△ABC中，tanA，tanB，tanC依次成等差数列，则B的取值范围是

A.
（0， $数学公式$ ]∪（ $数学公式$ ， $数学公式$ ]
B.
（0， $数学公式$ ]∪（ $数学公式$ ， $数学公式$ ]
C.
[ $数学公式$ ）
D.
[ $数学公式$ ， $数学公式$ ）

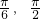D
分析：由已知先求出2tanB=tanA+tanC＞0，tanAtanC=3．再由（2tanB）²=（tanA+tanC）²=tan²A+tan²C+2tanAtanC≥4tanAtanC=12，求出 $\text{[math]}$ ，从而得到B的取值范围．
解答：由已知得2tanB=tanA+tanC＞0（显然tanB≠0，若tanB＜0，因为tanA＞0且tanC＞0，tanA+tanC＞0，这与tanB＜0矛盾），
又tanB=-tan（A+C）= $\text{[math]}$ ，所以tanAtanC=3．
又（2tanB）²=（tanA+tanC）²=tan²A+tan²C+2tanAtanC≥4tanAtanC=12，
因此tan²B≥3，又tanB＞0，所以 $\text{[math]}$ ， $\text{[math]}$ ，即B的取值范围是[ $\text{[math]}$ ），
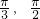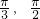故选D．
点评：本题借助等差数列的性质考查三解函数知识，体现了出题者的智慧，解题时要注意三角函数公式的灵活运用．

练习册系列答案

暑假学与练浙江科学技术出版社系列答案

新课堂暑假生活北京教育出版社系列答案

快乐暑假广西师范大学出版社系列答案

暑假自主学习手册江苏人民出版社系列答案

暑假生活江西高校出版社系列答案

暑假作业贵州人民出版社系列答案

暑假作业教育科学出版社系列答案

新课标暑假作业二十一世纪出版社系列答案

暑假作业期末综合复习东南大学出版社系列答案

书香天博暑假作业西安出版社系列答案

相关题目

在△ABC中，tan B=1，tan C=2，b=100，则a=_______．

在△ABC中，tan B=1，tan C=2，b=100，则a=__________．

在△ABC中，tan，＝0，则过点C，以A、H为两焦点的椭圆的离心率为

在△ABC中，tan＝，＝0，＝0，则过点C，以A、H为两焦点的椭圆的离心率为

在△ABC中，tan

=2sinC。
（1）求∠C的大小；
（2）求y=sinA+sinB+sinC的取值范围。