题目内容
(本小题满分12分)如图 是图
是图 的三视图,三棱锥
的三视图,三棱锥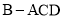 中,
中, ,
,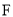 分别是棱
分别是棱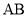 ,
, 的中点.
的中点.

(1)求证: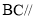 平面
平面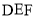 ;
;
(2)求三棱锥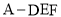 的体积.
的体积.
(1)见解析;(2) .
.
【解析】
试题分析:证明:(1)根据 分别是
分别是 的中点得到
的中点得到 ,应用判定定理即得证.
,应用判定定理即得证.
(2)由图1得 ⊥
⊥ ,
, ⊥
⊥ ,
, ⊥
⊥ ,得到
,得到 ⊥平面
⊥平面 .
.
取 的中点
的中点 ,连接
,连接 ,求得
,求得 =
= ,进一步计算体积.
,进一步计算体积.
试题解析:证明:(1)
 分别是
分别是 的中点
的中点



 平面
平面 ,
,
 平面
平面

 平面
平面 4分
4分

(2)∵如图1得 ⊥
⊥ ,
, ⊥
⊥ ,
, ⊥
⊥
又∵ ∩
∩ =
=
∴ ⊥平面
⊥平面 8分
8分
取 的中点
的中点 ,连接
,连接
∵ 是
是 的中点
的中点
∴

∴ ⊥平面
⊥平面
 =
=
∴ 12分
12分
考点:1.平行关系、垂直关系;2.几何体的体积.
考点分析: 考点1:柱、锥、台、球的表面积和体积 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
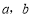 为实数,函数
为实数,函数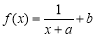 ,函数
,函数 .
.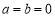 时,令
时,令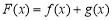 ,求函数
,求函数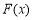 的极值;
的极值;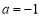 时,令
时,令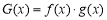 ,是否存在实数
,是否存在实数 ,使得对于函数
,使得对于函数 定义域中的任意实数
定义域中的任意实数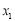 ,均存在实数
,均存在实数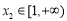 ,有
,有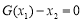 成立,若存在,求出实数
成立,若存在,求出实数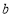 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.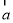 ,
, ,“
,“ ”是“
”是“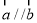 ”的( )
”的( ) ,
, ,则点
,则点 满足
满足 的概率为( )
的概率为( ) B.
B. C.
C. D.
D.
 ,那么判断框中应填入的关于
,那么判断框中应填入的关于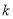 的条件是( )
的条件是( )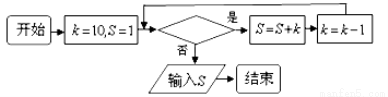
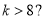 B.
B.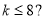 C.
C.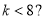 D.
D.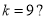
 的直线被圆
的直线被圆 所截得的弦长为 .
所截得的弦长为 .
 ,
,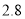 B.
B.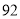 ,
,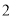 C.
C.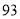 ,
,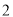 D.
D. ,
,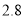
 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且满足
,且满足 ,则
,则 .
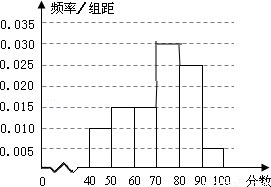
.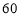 名同学将其成绩(百分制,均为整数)分成
名同学将其成绩(百分制,均为整数)分成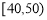 ,
,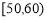 ,
,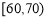 ,
,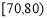 ,
,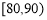 ,
, 六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.