题目内容
(1)求不等式的解集: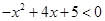 ;
;
(2)求函数的定义域: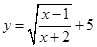 .
.
(1) ; (2)
; (2)
解析试题分析:(1)根据解一元二次不等式的步骤,首先求方程 ,
,
再结合函数 的图象写出不等式的解;
的图象写出不等式的解;
(2)已知解析式求函数的定义域,转化为解不等式 ,从而得到函数的定义域.
,从而得到函数的定义域.
试题解析:解:(1)解:原不等式等价于 ,
,
令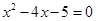 ,得
,得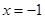 或
或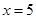
所以原不等式的解为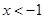 或
或 ,
,
即原不等式的解集为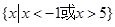
(2)要使函数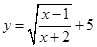 有意义,则
有意义,则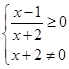 ,
,
得不等式组的解为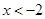 或
或 ,
,
所以原不等式的解集为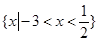 .
.
所以函数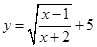 的定义域为
的定义域为
考点:1、一元二次不等式的解法;2、分式不等式的解法;3、函数的定义域.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
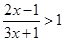 的解集是 .
的解集是 . .
.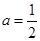 时,解不等式
时,解不等式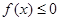 ;
; ,解关于
,解关于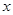 的不等式
的不等式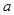 2+
2+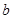 2恒成立,试求2
2恒成立,试求2 满足
满足 ,证明:
,证明: .
. 的不等式
的不等式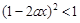 .
.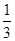 ,|2x-y|<
,|2x-y|< .求证:|y|<
.求证:|y|<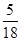 .
.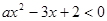 的解集为
的解集为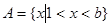 .
.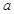 ,
, 的值;
的值;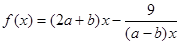
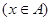 的最小值.
的最小值.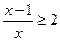 的解集是
的解集是