题目内容
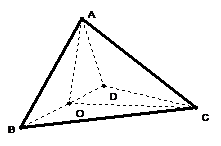 如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=![]()
(1)求证:AO![]() 平面BCD,(2)求异面直线AB与CD所成角的大小,(3)求两面角O—AC—D的大小。
平面BCD,(2)求异面直线AB与CD所成角的大小,(3)求两面角O—AC—D的大小。
(Ⅰ)见解析 (Ⅱ) ∠OEF=arccos![]() 。
。
(Ⅲ)arctan![]() .
.
解析:
:(1)证明:![]() AB=AD,BO=OD
AB=AD,BO=OD ![]() AO
AO![]() BD,连接OC,
BD,连接OC,
![]() CB=CD,BO=OD,
CB=CD,BO=OD, ![]() CO
CO![]() BD,
BD,![]() CO=
CO=![]() ,AO=1,又CA=2,
,AO=1,又CA=2,
![]()
![]() 即AO
即AO![]() OC,
OC,![]() ,
,![]() AO
AO![]() 平面BCD.
平面BCD.
(2)取BC的中点E,AC的中点F,∵O为BD的中点,∴EF∥AB,EO∥CD∴∠OEF或其补角是AB与CD所成的角,∴连接OF,∵OF是RT△AOC斜边AC上的中线,∴OF=![]() AC=1,∵EO=
AC=1,∵EO=![]() CD=1,EF=
CD=1,EF=![]() AB=
AB=![]() ,在△OEF中,由余弦定理得cos∠OEF=
,在△OEF中,由余弦定理得cos∠OEF=![]() ∴∠OEF=arccos
∴∠OEF=arccos![]() 。
。
(3)∵DO⊥OC,DO⊥AO,∴DO⊥平面AOC,过O作OG⊥AC于G连接DG
∴OG是DG在平面AOC上的射影,由三垂线定理得DG⊥AC,
∴∠OGD是二面角O—AC—D的平面角。
∵OG·AC=AO·OC,∴OG=![]() ,在RT△DOG中,tan∠DOG=
,在RT△DOG中,tan∠DOG=![]() ,
,
∴∠OGD=arctan![]() ,∴二面角O—AC—D为arctan
,∴二面角O—AC—D为arctan![]() .
.

练习册系列答案
相关题目
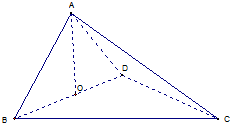 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.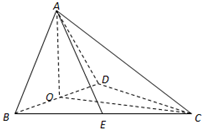 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.