题目内容
如图,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱的两端点异色.如果只有5种不同的颜色可供选择,那么不同的染色方法共有多少种?
解析:将四棱锥S-ABCD沿侧棱剪开展在同一平面上(如图),

由题设知,点S,A,B所染色互不相同,它们共有5×4×3=60种不同的染色方法.为叙述方便,把5种不同的颜色分别记为1,2,3,4,5.当S,A,B染好色后,不妨设它们分别染色为1,2,3.若C染色2,则D可染3,4,5中的任一种色,有3种染法;若C染色4,则D可染3或5,有2种染法;若C染色5,则D可染3或4,也有2种染法.根据分步原理,总的染色方法有N=60×(3+2+2)=420(种).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
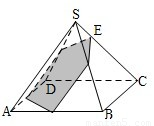
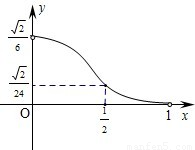
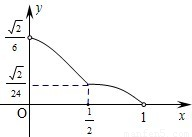
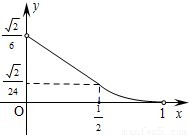
 (2012•江西)如图,已知正四棱锥S-ABCD所有棱长都为1,点E是侧棱SC上一动点,过点E垂直于SC的截面将正四棱锥分成上、下两部分.记SE=x(0<x<1),截面下面部分的体积为V(x),则函数y=V(x)的图象大致为( )
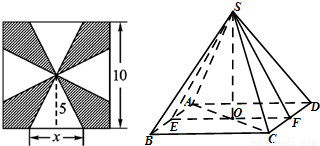
(2012•江西)如图,已知正四棱锥S-ABCD所有棱长都为1,点E是侧棱SC上一动点,过点E垂直于SC的截面将正四棱锥分成上、下两部分.记SE=x(0<x<1),截面下面部分的体积为V(x),则函数y=V(x)的图象大致为( ) 一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).
一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).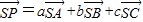 (a+b+c=1),在第(1)问的条件下,求
(a+b+c=1),在第(1)问的条件下,求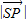 的最小值,并求取得最小值时a,b,c的值;
的最小值,并求取得最小值时a,b,c的值;