Question

（本小题满分12分）

如图，在底面是正方形的四棱锥P—ABCD中，平面PCD⊥平面ABCD，PC=PD=CD=2.

   （I）求证：PD⊥BC；

   （II）求二面角B—PD—C的大小.

Answer 1

（本小题满分12分）

方法一：

   （I）证明：∵平面PCD⊥平面ABCD，

又∵平面PCD∩平面ABCD=CD，

BC在平面ABCD内 ，BC⊥CD，

∴BC⊥平面PCD.

∴PD⊥BC.           …………6分

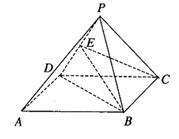
   （II）解：取PD的中点E，连接CE、BE，

为正三角形，

由（I）知BC⊥平面PCD，

∴CE是BE在平面PCD内的射影，

∴BE⊥PD.

∴∠CEB为二面角B—PD—C的平面角.  …………9分

在

∴二面角B—PD—C的大小为     …………12分

方法二：（I）证明：取CD的中点为O，连接PO，

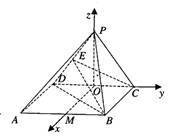
∵PD=PC，∴PO⊥CD，

∵平面PCD⊥平面ABCD，

平面PCD∩平面ABCD=CD，

∴PO⊥平面ABCD，

如图，在平面ABCD内，过O作OM⊥CD交AB于M，

以O为原点，OM、OC、OP分别为x、y、z轴，

建立空间直角坐标系O—xyz，

    由B（2，1，0），C（0，1，0），D（0，-1，0），     …………4分

    

                         …………6分

   （II）解：取PD的中点E，连接CE、BE，则

    为正三角形，

   

    为二面角B—PD—C的平面角. …………9分

   

    二面角B—PD—C的大小为    …………12分