题目内容

已知A、B、C是直线l上的三个定点,其中AB的长为a,BC的长为c.动点Pl,但P与l在确定的平面α内,且恒有∠APB=∠BPC,求动点P的轨迹.

解析:如图,以AC为x轴,以B为坐标原点建立直角坐标系.?

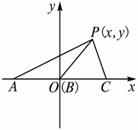
设P点的坐标为(x,y).?

由已知∠APB=∠BPC,?

得=.①?

设A(-a,0),C(c,0),a>0,c>0.

则|PA|=,

|PC|=.

将其代入①得=,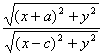

化简,得(a2-c2)x2+(a2-c2)y2-2ac(a+c)x=0.②?

当a=c时,方程②变为x=0,P点的轨迹为y轴(原点除外).?

当a≠c时,方程②?(a-c)x2+(a-c)y2-2acx=0

x2+y2-x=0

(x-)2+y2=()2.?

∴P点的轨迹是以(,0)为圆心,以为半径的圆.(除原点和点(,0)外)

练习册系列答案
相关题目
已知A、B、C是直线l上的不同三点，O是l外一点，向量
OA
，
OB
，
OC
满足
OA
=(
3
2
x2+1)
OB
-(lnx-y)
OC
，记y=f（x）；
（1）求函数y=f（x）的解析式；
（2）求函数y=f（x）的单调区间．
6、已知a、b、c是直线，α是平面，给出下列命题：
①若a∥b，b⊥c，则a⊥c；②若a⊥b，b⊥c，则a∥c；
③若a∥α，b?α，则a∥b；④若a⊥α，b?α，则a⊥b；
⑤若a与b异面，则至多有一条直线与a、b都垂直．
其中真命题是
①④
．（把符合条件的序号都填上）
已知A、B、C是直线l上不同的三点，O是l外一点，向量
OA
，
OB
，
OC
满足：
OA
-(
3
2
x2+1)•
OB
-[ln(2+3x)-y]•
OC
=
0
．记y=f（x）．
（Ⅰ）求函数y=f（x）的解析式：
（Ⅱ）若对任意x∈[
1
6
，
1
3
]，不等式|a-lnx|-ln[f'（x）-3x]＞0恒成立，求实数a的取值范围：
（Ⅲ）若关于x的方程f（x）=2x+b在（0，1]上恰有两个不同的实根，求实数b的取值范围．
已知a、b、c是直线，β是平面，给出下列命题：
①若a⊥b，b⊥c，则a∥c；
②若a∥b，b⊥c，则a⊥c；
③若a∥β，a?α，α∩β=b则a‖b；
④若a与b异面，且a∥β，则b与β相交；
其中真命题的序号是
②③
②③
．（要求写出所有真命题的序号）
已知A、B、C是直线l上的不同的三点，O是外一点，则向量
OA
、
OB
、
OC
满足：
OA
=λ
OB
+μ
OC
，其中λ+μ=1．
（1）若A、B、C三点共线且有
OA
-(3x+1)•
OB
-(
3
2+3x
-y)•
OC
=
0
成立．记y=f（x），求函数y=f（x）的解析式；
（2）若对任意x∈[
1
6
，
1
3
]，不等式|a-lnx|-ln[f（x）-3x]＞0恒成立，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网