Question

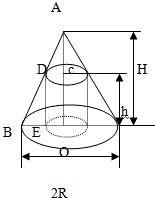
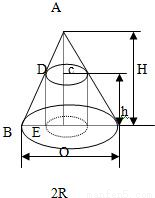
已知圆锥体的底面半径为R，高为H求内接于这个圆锥体并且体积最大的圆柱体的高h（如图）．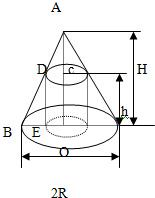

Answer 1

分析：先设出圆柱的底面半径，高为h，利用三角形相似，推出r的表达式，
然后求出体积表达式，利用均值不等式，求出体积最大值时的圆柱体的高h．

解答：解：设圆柱体半径为r高为h
由△ACD∽△AOB得

H-h

H

=

r

R

．
由此得r=

R

H

(H-h)，
圆柱体体积V(h)=πr2h=

πR2

H2

(H-h)2h．
由题意，H＞h＞0，利用均值不等式，有
原式=4•

πR2

H2

•

H-h

2

•

H-h

2

•h≤4•

πR2

H2

•

H3

27

=

4

27

πR2H．
当

H-h

2

=h，时上式取等号，因此当h=

H

3

时，V（h）最大．

点评：本题考查旋转体的体积，考查均值不等式求函数的最值，是中档题．