题目内容
如图所示,在正方体ABCD-A1B1C1D1中,AB=a,E为棱A1D1中点.
(I)求二面角E-AC-B的正切值;
(II)求直线A1C1到平面EAC的距离.
(I)求二面角E-AC-B的正切值;
(II)求直线A1C1到平面EAC的距离.

(I)取AD的中点H,连接EH,则EH⊥平面ABCD,过H作HF⊥AC与F,连接EF,
则EF在平面ABCD内的射影为HF,由三垂线定理得EF⊥AC,,
∴∠EFH即为

二面角E-AC-B的补角
∵EH=a,HF=
BD=
a
∴∠tan∠EFH=
=
=2
∴二面角E-AC-B的正切值为-2
…6分
(II)直线A1C1到平面EAC的距离,即A1点到平面EAC的距离d,…8分
∵VA1-EAC=VD-A1AE
∴S△EAC•d=SA1AE•CD
∵EF=
=
=
a
∴S△EAC=
•AC•EF=
•
a•
a=
a2
而SA1AE=
•
•a=
∴
a2•d=
•a
∴d=
∴直线A1C1到平面EAC的距离
则EF在平面ABCD内的射影为HF,由三垂线定理得EF⊥AC,,
∴∠EFH即为

二面角E-AC-B的补角
∵EH=a,HF=
| 1 |
| 4 |
| ||
| 4 |
∴∠tan∠EFH=
| EH |
| HF |
| a | ||||
|
| 2 |
∴二面角E-AC-B的正切值为-2
| 2 |
(II)直线A1C1到平面EAC的距离,即A1点到平面EAC的距离d,…8分
∵VA1-EAC=VD-A1AE
∴S△EAC•d=SA1AE•CD
∵EF=
| EH2+FH2 |
a2+(
|
3
| ||
| 4 |
∴S△EAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
3
| ||
| 4 |
| 3 |
| 4 |
而SA1AE=
| 1 |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
∴
| 3 |
| 4 |
| a2 |
| 4 |
∴d=
| a |
| 3 |
∴直线A1C1到平面EAC的距离
| a |
| 3 |

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
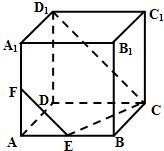 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
 (2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )
(2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( ) 如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为( )
如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为( )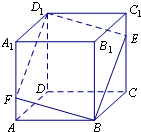 如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中假命题是( )
如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中假命题是( )