题目内容
定义在R上的偶函数f（x）在[0，+∞）上是减函数，若f（lgx）＞f（1），则x的取值范围是
- A.
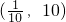
- B.
- C.
- D.（0，1）∪（10，+∞）
A
分析：根据f（x）是偶函数，f（1）＜f（lgx），可得f（1）＜f（|lgx|），再利用f（x）在区间[0，+∞）上是减函数，可得-1＜lgx＜1，从而可求x的取值范围．
解答：∵f（x）是偶函数，f（1）＜f（lgx），
∴f（1）＜f（|lgx|），
又∵f（x）在区间[0，+∞）上是减函数，
∴1＞|lgx|，
∴-1＜lgx＜1，
∴
∴x的取值范围是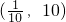
故选A．
点评：本题重点考查函数的奇偶性、单调性，考查解抽象不等式，解题的关键是利用函数的性质化抽象不等式为具体不等式．
分析：根据f（x）是偶函数，f（1）＜f（lgx），可得f（1）＜f（|lgx|），再利用f（x）在区间[0，+∞）上是减函数，可得-1＜lgx＜1，从而可求x的取值范围．
解答：∵f（x）是偶函数，f（1）＜f（lgx），
∴f（1）＜f（|lgx|），
又∵f（x）在区间[0，+∞）上是减函数，
∴1＞|lgx|，
∴-1＜lgx＜1，
∴
∴x的取值范围是
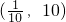
故选A．
点评：本题重点考查函数的奇偶性、单调性，考查解抽象不等式，解题的关键是利用函数的性质化抽象不等式为具体不等式．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知定义在R上的偶函数f（x）．当x≥0时，