题目内容
20. 如图,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知![]() 求
求
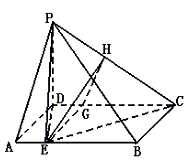
(Ⅰ)异面直线PD与EC的距离;
(Ⅱ)二面角E—PC—D的大小.
20.
解法一:
(Ⅰ)因PD⊥底面,故PD⊥DE,又因EC⊥PE,且DE
是PE在面ABCD内的射影,由三垂直线定理的逆定理知
EC⊥DE,因此DE是异面直线PD与EC的公垂线.
设DE=x,因△DAE∽△CED,故![]() (负根舍去).
(负根舍去).
从而DE=1,即异面直线PD与EC的距离为1.

(Ⅱ)过E作EG⊥CD交CD于G,作GH⊥PC交PC于H,连接EH.因PD⊥底面,
故PD⊥EG,从而EG⊥面PCD.
因GH⊥PC,且GH是EH在面PDC内的射影,由三垂线定理知EH⊥PC.
因此∠EHG为二面角的平面角.
在面PDC中,PD=![]() ,CD=2,GC=
,CD=2,GC=![]()
因△PDC∽△GHC,故![]() ,
,
又![]()
故在![]()
![]()
即二面角E—PC—D的大小为![]()
解法二:
(Ⅰ)以D为原点,![]() 、
、![]() 、
、![]() 分别为x、y、
分别为x、y、
z轴建立空间直角坐标系.
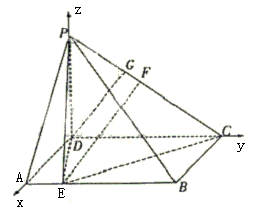
由已知可得D(0,0,0),P(0,0,![]() ,C(0,2,0)设
,C(0,2,0)设![]()
![]() 由
由![]()
![]() ·
·![]() =0,
=0,
即![]() 由
由![]() ·
·![]()
![]() ,
,
又PD⊥DE,故DE是异面直线PD与CE的公垂线,易得|![]() |=1,故异面直线PD、
|=1,故异面直线PD、
CE的距离为1.
(Ⅱ)作DG⊥PC,可设G(0,y,z).由 ![]() 得
得![]()
即![]()
![]() =(0,1,
=(0,1,![]() )作EF⊥PC于F,设F(0,m,n),
)作EF⊥PC于F,设F(0,m,n),
则![]() =
=![]()
由![]() ·
·![]()
![]() ,
,
又由F在PC上得![]()
![]()
![]()
因![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,故平面E—PC—D的平面角
,故平面E—PC—D的平面角![]() 的大小为向量
的大小为向量![]() 与
与![]() 的夹角.
的夹角.
故![]()
![]()
![]()
即二面角E—PC—D的大小为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
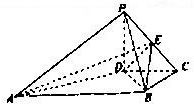 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,E为棱PC上异于C的一点,DE⊥BE.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,E为棱PC上异于C的一点,DE⊥BE.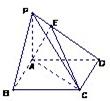 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E点满足
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E点满足 (2013•南通三模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等.
(2013•南通三模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等.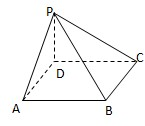 如图,在四棱锥P-ABCD中,底面ABCD是边长为的正方形,并且PD=,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是边长为的正方形,并且PD=,PA=PC= (2012•安徽模拟)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面四边形ABCD为直角梯形,∠B=∠C=90°,AB=3CD,∠PBC=30°,点M是PB上的动点,且
(2012•安徽模拟)如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面四边形ABCD为直角梯形,∠B=∠C=90°,AB=3CD,∠PBC=30°,点M是PB上的动点,且