题目内容

已知函数f（x）的定义域为D，若对任意x₁，x₂∈D，当x₁＜x₂时，都有f（x₁）≤f（x₂），则称函数f（x）在D上为非减函数．设函数f（x）在[0，1]上为非减函数，且满足以下三个条件：①f（0）=0；②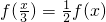 $数学公式$ ；③f（1-x）=2-f（x）．则 $数学公式$ =

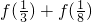A.
1
B.
$数学公式$
C.
2
D.
$数学公式$

B
分析：在③中，令x=0，则可求出f（1），在②中，令x=1，则可求出f（ $\text{[math]}$ ）．在②③中，再分别令x= $\text{[math]}$ ，可求出 $\text{[math]}$ ，函数f（x）在[0，1]上为非减函数，可得f（ $\text{[math]}$ ）≤f（ $\text{[math]}$ ）≤ $\text{[math]}$ ，进而求出 $\text{[math]}$ 的值．
解答：由③，令x=0，则f（1）=2-f（0）．又f（0）=0，∴f（1）=2．
由②令x=1，则f（ $\text{[math]}$ ）= $\text{[math]}$ ，∴ $\text{[math]}$ ．
在③中，令x= $\text{[math]}$ ，则f（1- $\text{[math]}$ ）=2-f（ $\text{[math]}$ ），解得f（ $\text{[math]}$ ）=1，
在②中，令x= $\text{[math]}$ ，则f（ $\text{[math]}$ ）= $\text{[math]}$ = $\text{[math]}$ ；再令x= $\text{[math]}$ ，则f（ $\text{[math]}$ ）= $\text{[math]}$ = $\text{[math]}$ ．
∵ $\text{[math]}$ ，且函数f（x）在[0，1]上为非减函数，
∴f（ $\text{[math]}$ ）≤f（ $\text{[math]}$ ）≤ $\text{[math]}$ ，∴ $\text{[math]}$ ．
于是 $\text{[math]}$ ．
故选B．
点评：本题考查了满足某些条件的非减函数，恰当的取值和利用条件非减函数是解决此题的关键．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

已知函数f（x）=log₃

，M(x1，y1)，N(x2，y2)是f（x）图象上的两点，横坐标为

（O为坐标原点）．
（Ⅰ）求证：y₁+y₂为定值；
（Ⅱ）若Sn=f(

)，其中n∈N^*，且n≥2，求S_n；
（Ⅲ）已知a_n=

4(Sn+1)(Sn+1+1)

，其中n∈N^*，T_n为数列{a_n}的前n项和，若T_n＜m（S_n+1+1）对一切n∈N^*都成立，试求m的取值范围．

下列说法正确的有（　　）个．
①已知函数f（x）在（a，b）内可导，若f（x）在（a，b）内单调递增，则对任意的?x∈（a，b），有f′（x）＞0．
②函数f（x）图象在点P处的切线存在，则函数f（x）在点P处的导数存在；反之若函数f（x）在点P处的导数存在，则函数f（x）图象在点P处的切线存在．
③因为3＞2，所以3+i＞2+i，其中i为虚数单位．
④定积分定义可以分为：分割、近似代替、求和、取极限四步，对求和In=

f(ξi)△x中ξ_i的选取是任意的，且I_n仅于n有关．
⑤已知2i-3是方程2x²+px+q=0的一个根，则实数p，q的值分别是12，26．

已知函数f（x）=sin（2x-

），g（x）=sin（2x+

），直线y=m与两个相邻函数的交点为A，B，若m变化时，AB的长度是一个定值，则AB的值是（　　）

（Ⅰ）已知函数f（x）=x³-x，其图象记为曲线C．
（i）求函数f（x）的单调区间；
（ii）证明：若对于任意非零实数x₁，曲线C与其在点P₁（x₁，f（x₁））处的切线交于另一点P₂（x₂，f（x₂）），曲线C与其在点P₂（x₂，f（x₂））处的切线交于另一点P₃（x₃，f（x₃）），线段P₁P₂，P₂P₃与曲线C所围成封闭图形的面积记为S₁，S₂．则

为定值；
（Ⅱ）对于一般的三次函数g（x）=ax³+bx²+cx+d（a≠0），请给出类似于（Ⅰ）（ii）的正确命题，并予以证明．

已知函数f（x）=x³-ax+b存在极值点．
（1）求a的取值范围；
（2）过曲线y=f（x）外的点P（1，0）作曲线y=f（x）的切线，所作切线恰有两条，切点分别为A、B．
（ⅰ）证明：a=b；
（ⅱ）请问△PAB的面积是否为定值？若是，求此定值；若不是求出面积的取值范围．