题目内容

已知△ABC，若对任意k∈R，有| 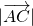$数学公式$ |≥ $数学公式$ ，则△ABC一定是

A.
直角三角形
B.
钝角三角形
C.
锐角三角形
D.
以上均有可能

A
分析：图中BC′的长度就是| $\text{[math]}$ |，要使不等式成立，则|AC|必须是BC′的最小值，即AC垂直BC，故角C为直角．
解答：

解：当k为任意实数时，那么k $\text{[math]}$ 的方向有可能向左，也可能向右．长度也是不确定的，
图中BC′的长度就是| $\text{[math]}$ |，可以看出，当BC′垂直CB时，| $\text{[math]}$ |有最小值，要使不等式成立，
则|AC|必须是BC′的最小值，即AC垂直BC，故角C为直角，
故选A．
点评：本题考查两个向量的加减法的法则，以及其几何意义，判断三角形的形状的方法，判断|AC|必须是BC′的最小值，是
解题的关键．

练习册系列答案

高效课堂课时作业系列答案

ABC考王全优卷系列答案

高分拔尖提优密卷系列答案

金钥匙课时学案作业本系列答案

特别培优训练系列答案

课堂作业讲与练系列答案

学海单元双测第一卷系列答案

完全考卷系列答案

同步课课练每课一练系列答案

新编教与学系列答案

相关题目

给出下列命题：

①某校开设A类选修课3门，B类选修课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有60种；

②对于任意实数x，有f(－x)＝－f(x)，g(－x)＝g(x)，且x＞0时，(x)＞0，＞0，则x＜0时，(x)＞(x)；

③已知点M在平面ABC内，并且对空间任一点O，＝x＋＋，则的值为1；

④在正三棱柱ABC－A₁B₁C₁中，若AB＝2，AA₁＝1，则点A到平面A₁BC的距离为，其中正确命题的序号是________．

给出下列命题：

①某校开设A类选修课3门，B类选修课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有60种；

②对于任意实数x，有f(－x)＝－f(x)，g(－x)，且x＞0时，(x)＞0，(x)＞0，则x＜0时，(x)＞(x)；

③已知点M在平面ABC内，并且对空间任一点O，＝x＋＋，则x的值为1；

④在正三棱柱ABC－A₁B₁C₁中，若AB＝2，AA₁＝1，则点A到平面A₁BC的距离为，其中正确命题的序号是________