题目内容
(本题满分12分)如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
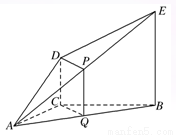
(1)证明:PQ∥平面ACD;
(2)求AD与平面ABE所成角的正弦值.
(1)见解析;(2)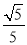
【解析】
试题分析:(1)证明:因为P,Q分别为AE,AB的中点,
所以PQ∥EB.又DC∥EB,因此PQ∥DC,
又PQ?平面ACD,
从而PQ∥平面ACD.
(2)如图,
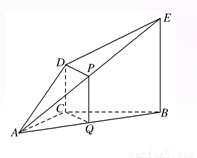
连接CQ,DP,因为Q为AB的中点,且AC=BC,所以CQ⊥AB.
因为DC⊥平面ABC,
EB∥DC,
所以EB⊥平面ABC,因此CQ⊥EB.[来
故CQ⊥平面ABE.
由(1)有PQ∥DC,又PQ=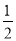 EB=DC,
EB=DC,
所以四边形CQPD为平行四边形,故DP∥CQ.
因此DP⊥平面ABE,∠DAP为AD和平面ABE所成的角,
在Rt△DPA中,AD=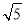 ,DP=1,
,DP=1,
sin∠DAP=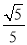 ,
,
因此AD和平面ABE所成角的正弦值为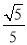 .
.
考点:本题考查集合的交集,并集的运算,集合与集合的关系

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
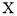 的分布列为
的分布列为







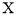 的数学期望
的数学期望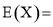 ( )
( )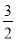 B.
B.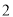 C.
C. D.
D.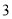
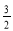 D.
D.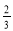

 中,
中, ,且
,且 ,则
,则 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
 共线,则t= .
共线,则t= .