题目内容
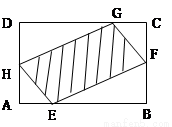
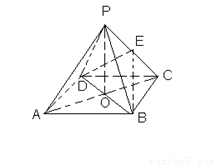
(本题8分)如图,ABCD是正方形,O是正方形的中心, PO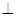 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE (2)平面PAC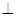 平面BDE
平面BDE
【答案】
见解析。
【解析】本题主要考查中位线定理、线面平行的判定定理和面面垂直的判定定理.考查立体几何的基本定理和空间想象能力
(1)先根据中位线定理得到OE∥AP,进而再由线面平行的判定定理可得到PA∥平面BDE.
(2)先根据线面垂直的性质定理得到PO⊥BD,结合AC⊥BD根据线面垂直的判定定理得到BD⊥平面PAC,从而根据面面垂直的判定定理得到平面PAC⊥平面BDE,得证.
证明:(1)连结E0
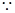 四边形ABCD为正方形
四边形ABCD为正方形
 O为AC的中点 又E是PC的中点
O为AC的中点 又E是PC的中点
 EO//PA
EO//PA

 PA//平面BDE
4分
PA//平面BDE
4分
(2)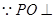 平面ABCD,
平面ABCD,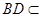 平面ABCD
平面ABCD

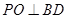
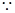 四边形ABCD是正方形
四边形ABCD是正方形

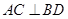


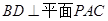 ,又
,又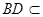 平面BDE
平面BDE
 平面PAC
平面PAC 平面BDE
4分
平面BDE
4分

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
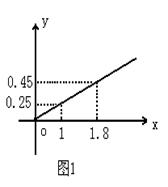
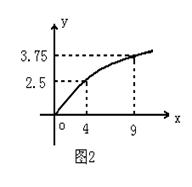
 示为投资的函数,并写出它们的函数关系式
示为投资的函数,并写出它们的函数关系式