题目内容
如图，O为坐标原点，过点P（2，0）且斜率为k的直线l交抛物线y2=2x于M（x1，y1），N（x2，y2）两点．
（1）写出直线l的方程；
（2）求x1x2与y1y2的值；
（3）求证：OM⊥ON．
解答：
（Ⅰ）解：直线l过点P（2，0）且斜率为k，故可直接写出直线l的方程为y=k（x﹣2） （k≠0）①
（Ⅱ）解：由①及y2=2x消去y代入可得k2x2﹣2（k2+1）x+4k2=0．②
则可以分析得：点M，N的横坐标x1与x2是②的两个根，
由韦达定理得
又由y12=2x1，y22=2x2得到（y1y2）2=4x1x2=4×4=16，又注意到y1y2＜0，
所以y1y2=﹣4．
（Ⅲ）证明：设OM，ON的斜率分别为k1，k2，
，
所以证得：OM⊥ON．
练习册系列答案
阅读快车系列答案
相关题目
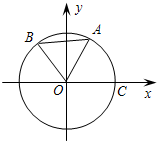如图，O为坐标原点，点A，B，C均在⊙O上，点A
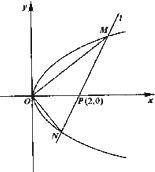如图，O为坐标原点，过点P（2，0）且斜率为k的直线l交抛物线y2=2x于M（x1，y1），N（x2，y2）两点．
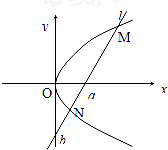如图，O为坐标原点，直线l在x轴和y轴上的截距分别是a和b，且交抛物线y2=2px（p＞0）于M（x1，y1）、N（x2，y2）两点（异于原点）．
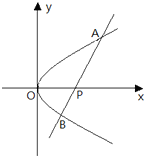（文）如图，O为坐标原点，过点P（2，0）且斜率为k的直线l交抛物线y2=2x于A（x1，y1），B（x2，y2）两点．
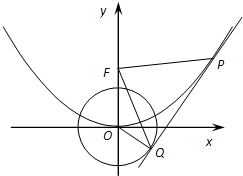如图，O为坐标原点，点F为抛物线C1：x2=2py（p＞0）的焦点，且抛物线C1上点P处的切线与圆C2：x2+y2=1相切于点Q．