题目内容
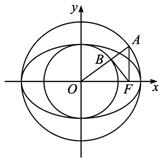
如图，椭圆
=1(a＞b＞c)的右准线l与x轴的交点为A，椭圆的上顶点为B，过椭圆的右焦点F作垂直于椭圆长轴的直线交椭圆于P点.若点D满足
(λ≠0).
(Ⅰ)求椭圆的离心率；
(Ⅱ)若椭圆的长轴长等于4，Q是椭圆右准线l上异于点A的任意一点，A1、A2分别是椭圆的左、右顶点，直线QA1、QA2与椭圆的另一个交点分别为M、N，求证：直线MN与x轴交于定点.
解：(Ⅰ)∵椭圆方程为
，(a＞b＞0，c＞0，c2=a2-b2)
∴A(,0)
F(c，0)，B(0，b)，P(c,)，
∵
∴D为FP的中点
∴D点坐标为(c,
)
∵
∴D在线段AB上
∵直线AB的方程为：
=1
∴c·
=1
化简得 3a2=4c2
∴e=
(Ⅱ)∵椭圆的长轴长等于4，∴a=2，b=1，c=
设直线QA1和QA2斜率分别为k1，k2，则由
(1+
)x2+16
x+16
-4=0
解得 xM=
由
(1+4
)x2-16
x+16
-4=0
解得 xN=
直线MN的方程为
，令y=0
得x=
化简得 x=2×
∵yQ=k1(
+2)=k2(
-2)
∴
∴
∴x=2
即直线MN与x轴交于定点(
,0).
练习册系列答案
相关题目
（a＞b＞0）的一个焦点为F(1,0)，且过点（2，0）.
=1（a＞b＞0）与过A（2，0），B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
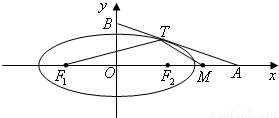
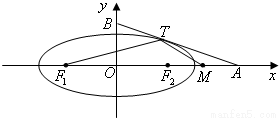如图，椭圆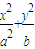
=1（a＞b＞0）与过点A（2，0）B（0，1）的直线有且只有一个公共点T，且椭圆的离心率e=
．
+
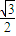=1(a＞b＞0)的中心O为圆心，分别以a和b为半径作大圆和小圆，过椭圆右焦点F(c,0)(c＞b)作垂直于x轴的直线交大圆于第一象限内的点A，连结OA交小圆于点B，设直线BF是小圆的切线.
·
=
b2.