题目内容
已知向量![]() ,
,![]() ,其中
,其中![]() ,设
,设![]() ,且函数
,且函数![]() 的最大值为
的最大值为![]() .
.
Ⅰ.求函数![]() 的解析式;
的解析式;
Ⅱ.设![]() ,求函数
,求函数![]() 的最大值和最小值以及对应的
的最大值和最小值以及对应的![]() 值;
值;
Ⅲ.若对于任意的实数![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围
的取值范围
Ⅰ
Ⅱ ![]()
Ⅲ ![]()
解析:
Ⅰ.由题意知![]()
![]() ,
,
令![]() ,则
,则![]() ,从而
,从而![]() ,
,
对称轴为![]() .
.
①当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ;
;
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
∴![]() ;
;
③当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ;
;
综上,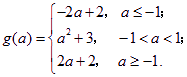 ………………4分
………………4分
Ⅱ.由![]() 知,
知,![]() .
.
又因为![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,∵
上单调递增,∵![]() ∴
∴
![]() ,此时
,此时![]() ;
;
![]() ,此时
,此时![]() . ………………7分
. ………………7分
Ⅲ.当![]() 时,
时,![]() 得
得![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() 得
得![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,得
,得![]() ,
,
令![]() ,则对称轴为
,则对称轴为![]() ,下面分情况讨论:
,下面分情况讨论:
①当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 上单调递增,从而只须
上单调递增,从而只须
![]() 即可,解得
即可,解得![]() ,从而
,从而![]() ;
;
②当![]() 时,即
时,即![]() ,只须
,只须![]() ,解得
,解得
![]() ,从而
,从而![]() ;
;
③当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 上单调递减,从而只须
上单调递减,从而只须
![]() 即可,解得
即可,解得![]() ,从而
,从而![]() ;
;
综上,实数![]() 的取值范围是
的取值范围是![]() . ………………10分
. ………………10分

练习册系列答案
相关题目
 ,
, ,其中
,其中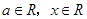 ,设
,设 ,且函数
,且函数 的最大值为
的最大值为 .。
.。 ,求函数
,求函数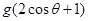 的最大值和最小值以及对应的
的最大值和最小值以及对应的 值。
值。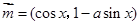 ,
,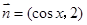 ,其中
,其中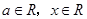 ,设
,设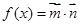 ,且函数
,且函数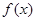 的最大值为
的最大值为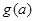 。
。 ,求函数
,求函数 的最大值和最小值以及对应的
的最大值和最小值以及对应的 值;
值;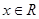 ,
,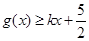 恒成立,求实数
恒成立,求实数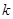 的取值范围。
的取值范围。