题目内容
已知函数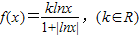
，且f（1og23）=1，则f（1og32）=1的值等于（ ）A．-1
B．1
C．0
D．与k有关
【答案】分析：由于log32=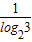
，只要寻求当a，b互为倒数时函数值的关系即可求解
解答：解：设ab=1，a＞0，b＞0，则f（a）=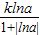
∴f（b）=f（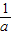
）=
=
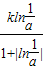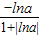=-f（a）
∵f（log23）=1，
∴f（log32）=f（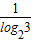
）=-1
故选A
点评：本题主要考查了对数函数的函数值的求解的应用，解题的关键是发现当ab=1时，f（b）=f（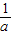
）=-f（a）．
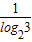，只要寻求当a，b互为倒数时函数值的关系即可求解解答：解：设ab=1，a＞0，b＞0，则f（a）=
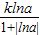
∴f（b）=f（
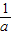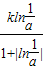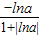）===-f（a）∵f（log23）=1，
∴f（log32）=f（
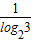）=-1故选A
点评：本题主要考查了对数函数的函数值的求解的应用，解题的关键是发现当ab=1时，f（b）=f（
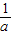）=-f（a）． 
练习册系列答案
相关题目
，且f（1）=2，
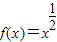，且f（2x-1）＜f（3x），则x的取值范围是 ．
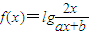，且f（1）=0，当x＞0时，恒有
．
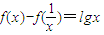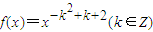，且f（2）＜f（3）
．若存在，求出这个p的值；若不存在，说明理由．
，且f(a)＝3，则a =