题目内容
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,过F2的直线交双曲线的右支于A,B两点,若△ABF1是以A为直角顶点的等腰三角形,e为双曲线的离心率,则e2=5-2$\sqrt{2}$.分析 可设|F1F2|=2c,|AF1|=m,若△ABF1构成以A为直角顶点的等腰直角三角形,则|AB|=|AF1|=m,|BF1|=$\sqrt{2}$m,再由双曲线的定义,可得m,再由勾股定理,可得a,c的方程,运用离心率公式计算即可得到.
解答 解:设|AF2|=m,由|AF1|-|AF2|=2a,
∴|AF1|=2a+|AF2|=2a+m,
又|AF1|=|AB|=|AF2|+|BF2|=m+|BF2|,
∴|BF2|=2a,又|BF1|-|BF2|=2a,
∴|BF1|=4a,
依题意$|{B{F_1}}|=\sqrt{2}|{A{F_1}}|$,即$4a=\sqrt{2}({2a+m})$,$m=2({\sqrt{2}-1})a$,
在Rt△F1AF2中${|{A{F_1}}|^2}+{|{A{F_2}}|^2}=4{c^2}$,即$8{a^2}+{({2\sqrt{2}a-2a})^2}=4{c^2}$,
即${c^2}=5{a^2}-2\sqrt{2}{a^2}$,∴e2=$5-2\sqrt{2}$.
故答案为:5-2$\sqrt{2}$.
点评 本题考查双曲线的定义、方程和性质,主要考查离心率的求法,同时考查勾股定理的运用,灵活运用双曲线的定义是解题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
16.将正奇数1,3,5,7,…按如表的方式进行排列,记aij表示第i行第j列的数,若aij=2015,则i+j的值为( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 1 | 3 | 5 | 7 | |
| 第2行 | 15 | 13 | 11 | 9 | |
| 第3行 | 17 | 19 | 21 | 23 | |
| 第4行 | 31 | 29 | 27 | 25 | |
| 第5行 | 39 | 37 | 35 | 33 | |
| … | … | … | … | … | … |
| A. | 505 | B. | 506 | C. | 254 | D. | 253 |
18.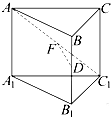 在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
 在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
在棱长均相等的正三棱柱ABC-A1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:①AC1⊥BC;②AF=FC1;③平面DAC1⊥平面ACC1A1,其中正确的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
9.如图几何体中,棱柱有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{3}=1$的离心率为2,则此双曲线的顶点到渐近线的距离等于( )
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |