题目内容
已知f(x)= x3-2ax2-3x(a∈R).
x3-2ax2-3x(a∈R).
(I)当|a|≤ 时,求证f(x)在(-1,1)内是减函数;
时,求证f(x)在(-1,1)内是减函数;
(Ⅱ)若y=f(x)在(-1,1)内有且只有一个极值点,求a的取值范围.
解:(I)∵f(x)= x3-2ax2-3x
x3-2ax2-3x
∴f′(x)=x2-4ax-3
∵|a|≤ ,
,
∴f′(-1)≤0,f′(1)≤0
∵f′(x)的图象开口向上,
∴在(-1,1)内.f(x)是一个减函数.
(II)设极值点x0,
∴f(x)在(-1,x0)上是增函数,在(x0,1)上是减函数,
∴a 时,f(x)在(-1,1)上有一个极值点,且是极大值点,
时,f(x)在(-1,1)上有一个极值点,且是极大值点,
a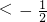 时,f(x)在(-1,1)上有一个极小值点,
时,f(x)在(-1,1)上有一个极小值点,
- ,f(x)在(-1,1)上没有极值点,
,f(x)在(-1,1)上没有极值点,
总上可知的取值范围是(-
分析:(I)首先对于函数求导,得到导函数是一个二次函数,根据二次函数的性质对于导函数的符号进行验证,得到结果.
(II)设出极值点,根据函数在所给的区间上只有一个极值点,对于函数的导函数的符号进行讨论,得到结果.
点评:本题考查函数的极值和单调性的应用,解题的关键是对于字母系数a的讨论,注意讨论的过程中做到不重不漏.
 x3-2ax2-3x
x3-2ax2-3x∴f′(x)=x2-4ax-3
∵|a|≤
 ,
,∴f′(-1)≤0,f′(1)≤0
∵f′(x)的图象开口向上,
∴在(-1,1)内.f(x)是一个减函数.
(II)设极值点x0,
∴f(x)在(-1,x0)上是增函数,在(x0,1)上是减函数,
∴a
 时,f(x)在(-1,1)上有一个极值点,且是极大值点,
时,f(x)在(-1,1)上有一个极值点,且是极大值点,a
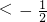 时,f(x)在(-1,1)上有一个极小值点,
时,f(x)在(-1,1)上有一个极小值点,-
 ,f(x)在(-1,1)上没有极值点,
,f(x)在(-1,1)上没有极值点,总上可知的取值范围是(-

分析:(I)首先对于函数求导,得到导函数是一个二次函数,根据二次函数的性质对于导函数的符号进行验证,得到结果.
(II)设出极值点,根据函数在所给的区间上只有一个极值点,对于函数的导函数的符号进行讨论,得到结果.
点评:本题考查函数的极值和单调性的应用,解题的关键是对于字母系数a的讨论,注意讨论的过程中做到不重不漏.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目