题目内容
四面体ABCD的四个顶点在同一球面上，AB=BC=CD=DA=3，AC=2
，BD=
，则该球的表面积为（ ）
| 3 |
| 6 |
分析：取BD中点F，AC中点E，由等腰三角形三线合一，及线面垂直的判定定理，可得BD⊥面AFC，及AC⊥面BED．由韦达定理可得BE=DE=
，EF=
，结合EF=
+
，可得球的半径R，进而得到球的表面积
| 6 |
3
| ||
| 2 |
| R2-AE2 |
| R2-BF2 |
解答：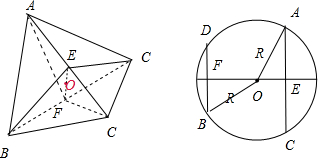
解：如左图，取BD中点F，AC中点E
由AB=BC=CD=DA=3，可得
CF⊥BD，AF⊥BD，
又∵CF∩AF=F，CF，AF?平面AFC，
故BD⊥面AFC
同理AC⊥面BED
故球心O必位于两垂直平面面AFC和面BED的交线EF上
又∵AC=2
，BD=
故BE=DE=
，EF=
设外接球半径为R，如右图（△AEO与△BFO不在同一平面）
利用EF=
+
解得R=
故该球的表面积S=4πR2=14π．
故选A
解：如左图，取BD中点F，AC中点E由AB=BC=CD=DA=3，可得
CF⊥BD，AF⊥BD，
又∵CF∩AF=F，CF，AF?平面AFC，
故BD⊥面AFC
同理AC⊥面BED
故球心O必位于两垂直平面面AFC和面BED的交线EF上
又∵AC=2
| 3 |
| 6 |
故BE=DE=
| 6 |
3
| ||
| 2 |
设外接球半径为R，如右图（△AEO与△BFO不在同一平面）
利用EF=
| R2-AE2 |
| R2-BF2 |
解得R=
| ||
| 2 |
故该球的表面积S=4πR2=14π．
故选A
点评：本题考查的知识点是球内接多面体，球的表面积，其中分析出球心O必位于两垂直平面面AFC和面BED的交线EF上，是解答的关键．
练习册系列答案
天天向上口算本系列答案
相关题目
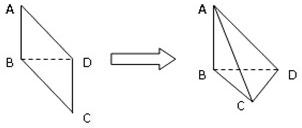
如图，已知四面体ABCD的四个面均为锐角三角形，EFGH分别是边AB，BC，CD，DA上的点，BD||平面EFGH，且EH=FG．
(a＋b＋c)r”，拓展到空间，类比上述结论，“若四面体ABCD的四个面的面积分别为S1，S2，S3，S4，内切球的半径为r，则四面体的体积为________”．