题目内容
已知函数f(x)=ax(a>0且a≠1)在区间[-2,2]上的值不大于2,则函数g(a)=log2a的值域是
- A.

- B.

- C.

- D.

A
分析:分a>1和0<a<1两种情况讨论,利用a>1时增,0<a<1时减可得a,再利用对数函数的单调性来解题
解答:∵函数f(x)=ax(a>0且a≠1)当a>1时,f(x)=ax区间[-2,2]上是增函数,
最大值为f(2)=a2≤2,得1<a≤ ∴
∴
g(a)=log2a∈(0, ]当0<a<1时,f(x)=ax区间[-2,2]上是减函数,
]当0<a<1时,f(x)=ax区间[-2,2]上是减函数,
最大值为f(-2)=a-2≤2,得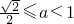 ,∴g(a)=log2a∈[-
,∴g(a)=log2a∈[- ,0]
,0]
故选 A
点评:指数函数f(x)=ax的单调性与底数有关,当底数与1的大小不确定时应注意分类讨论
分析:分a>1和0<a<1两种情况讨论,利用a>1时增,0<a<1时减可得a,再利用对数函数的单调性来解题
解答:∵函数f(x)=ax(a>0且a≠1)当a>1时,f(x)=ax区间[-2,2]上是增函数,
最大值为f(2)=a2≤2,得1<a≤
 ∴
∴g(a)=log2a∈(0,
 ]当0<a<1时,f(x)=ax区间[-2,2]上是减函数,
]当0<a<1时,f(x)=ax区间[-2,2]上是减函数,最大值为f(-2)=a-2≤2,得
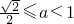 ,∴g(a)=log2a∈[-
,∴g(a)=log2a∈[- ,0]
,0]故选 A
点评:指数函数f(x)=ax的单调性与底数有关,当底数与1的大小不确定时应注意分类讨论

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目