题目内容
已知函数![]() ,
,![]() .(e=2.718…)
.(e=2.718…)
(I)求函数![]() 的极大值;(II )求证:
的极大值;(II )求证:![]() ;
;
(Ⅲ)对于函数![]() 与
与![]() 定义域上的任意实数
定义域上的任意实数![]() ,若存在常数
,若存在常数![]() ,使得
,使得![]() 和
和![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的“分界线”.设函数
的“分界线”.设函数![]() ,试探究函数
,试探究函数![]() 与
与![]() 是否存在“分界线”?若存在,请加以证明,并求出
是否存在“分界线”?若存在,请加以证明,并求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ) -2 (Ⅱ) 见解析 (Ⅲ)见解析
解析:
(Ⅰ)∵![]() ,∴
,∴![]() .……1分
.……1分
令![]() ,解得:
,解得:![]() ,令
,令![]() ,解得:
,解得:![]() ,…………………2分
,…………………2分
∴函数![]() 在
在![]() 上递增,
上递增,![]() 上递减,∴
上递减,∴![]() .……4分
.……4分
(Ⅱ)证明:由(1)知![]() 是函数
是函数![]() 极大值点,也是最大值点, ∴
极大值点,也是最大值点, ∴![]() ,
,
即![]() ,(当且仅当
,(当且仅当![]() 时等号成立)…………5分
时等号成立)…………5分
令![]() 得:
得:![]() , 取
, 取![]() ,
,
则![]() ,………………………………………………7分
,………………………………………………7分
∴![]() ,
,
迭加得![]() …………8分
…………8分
(Ⅲ)设![]() ,
,
则![]() .
.
∴当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
![]() ∴
∴![]() 是函数
是函数![]() 的极小值点,也是最小值点,∴
的极小值点,也是最小值点,∴![]()
∴函数![]() 与
与![]() 的图象在
的图象在![]() 处有公共点
处有公共点![]() .………………9分
.………………9分
设![]() 与
与![]() 存在 “分界线”且方程为:
存在 “分界线”且方程为:![]() .
.
令函数![]() ,
,
ⅰ)由![]() 在
在![]() 恒成立,
恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 成立,
成立,
∴![]() ,故
,故![]() .……………………………………11分
.……………………………………11分
ⅱ)下面再证明:![]() 恒成立.
恒成立.
设![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;当
单调递增;当![]() 时,
时,![]() .函数
.函数![]() 单调递减.
单调递减.
∴![]() 时
时![]() 取得最大值0,则
取得最大值0,则![]()
![]() 成立.…………13分
成立.…………13分
综上ⅰ)和ⅱ)知:![]() 且
且![]() ,
,
故函数![]() 与
与![]() 存在分界线为
存在分界线为![]() ,此时
,此时![]() .…………14分
.…………14分
另解:令![]() 则
则![]() ,探究得两函数图象的交点为
,探究得两函数图象的交点为![]() ,
,
设存在“分界线”且为:![]() ,令函数
,令函数![]() ,
,
再证:![]() 恒成立;
恒成立;![]() 恒成立。。。。。证法同上ⅰ)和ⅱ).
恒成立。。。。。证法同上ⅰ)和ⅱ).

练习册系列答案
相关题目
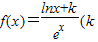 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行. 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行. 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行. 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行. 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.