题目内容
在等差数列{an}中,Sn为数列{an}的前n项和,a2=3,Sn-Sn-3=51(n>3),Sn=100,则n=________.
10
分析:依题意可求得an-1=17(n≥2),结合a2=3,Sn=100,利用等差数列的性质即可求得n的值.
解答:∵Sn-Sn-3=51(n>3),∴an+an-1+an-2=51(n>3).
又数列{an}为等差数列,∴3an-1=51(n≥2),∴an-1=17 (n≥2).
又a2=3,Sn=100,
Sn=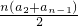 =
=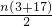 =100,解得 n=10,
=100,解得 n=10,
故答案为 10.
点评:本题考查数列的求和,突出等差等差数列的性质,考查观察与利用差等差数列的性质分析解决问题的能力,属于中档题.
分析:依题意可求得an-1=17(n≥2),结合a2=3,Sn=100,利用等差数列的性质即可求得n的值.
解答:∵Sn-Sn-3=51(n>3),∴an+an-1+an-2=51(n>3).
又数列{an}为等差数列,∴3an-1=51(n≥2),∴an-1=17 (n≥2).
又a2=3,Sn=100,
Sn=
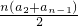 =
=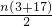 =100,解得 n=10,
=100,解得 n=10,故答案为 10.
点评:本题考查数列的求和,突出等差等差数列的性质,考查观察与利用差等差数列的性质分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目